当前位置：试卷中心 > 试卷详情

2022-2023学年辽宁省名校联盟高三（上）月考数学试卷（11月份）

发布：2024/8/2 8:0:9

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知集合
A
=
{
x
∈
N
|
4
-
x
＞
0
}
，B={x∈R|x²-4x＞0}，则A∩（∁_RB）=（　　）
A．{0，1，2，3，4} B．{0，1，2，3} C．{1，2，3，4} D．{1，2，3}
组卷：185引用：3难度：0.7
解析
2．已知复数
z
=
a
+
4
i
2
+
i
，若z是纯虚数，则实数a的值为（　　）
A．2 B．-1 C．-2 D．-8
组卷：13引用：2难度：0.8
解析
3．已知幂函数f（x）=（m²-m-1）x^-4m-3在（0，+∞）上是减函数，则实数m的值为（　　）
A．2 B．0 C．-1 D．-1或2
组卷：27引用：2难度：0.7
解析
4．已知
sin
（
α
-
π
6
）
=
1
3
，则
cos
（
2
α
+
2
π
3
）
的值为（　　）
A．
-
7
9
B．
-
1
3
C．
1
3
D．
7
9
组卷：86引用：9难度：0.9
解析
5．一项运输工程，若干辆运输车如果同时参加，需要24小时完成．如果每辆车开始参加运输的时间不同，每隔固定的时间有一辆车参加，参加后就一直运输到最后，那么第一辆车运输的时间恰为最末一辆车运输时间的5倍，按照这样的干法从开始到结束，需要的时间为（　　）
A．36小时 B．40小时 C．44小时 D．48小时
组卷：5引用：2难度：0.6
解析
6．已知正三棱台两底面边长分别为2，4，侧棱长为2，则该棱台的体积为（　　）
A．
8
2
3
B．
8
3
3
C．
3
2
D．
14
2
3
组卷：19引用：2难度：0.7
解析
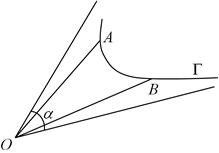7．如图，对于曲线Γ所在平面内的点O，若存在以O为顶点的角α，使得对于曲线Γ上的任意两个不同的点A，B恒有∠AOB≤α成立，则称角α为曲线Γ的相对于点O的“界角”，并称其中最小的“界角”为曲线Γ的相对于点O的“确界角”．已知曲线
C
：
y
=
x
e
x
-
1
+
1
，
x
≥
0
，
4
x
2
+
x
+
1
，
x
＜
0
（其中e=2.71828⋯是自然对数的底数），O为坐标原点，则曲线C的相对于点O的“确界角”为（　　）
A．
π
6
B．
π
4
C．
π
3
D．
π
2
组卷：126引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

21．已知正项数列{a_n}，{b_n}满足a₁=1，b₁=2，a_n，b_n，a_n+1成等比数列，b_n，a_n+1，b_n+1成等差数列．
（1）求数列{a_n}和{b_n}的通项公式；
（2）设
c
n
=
a
n
+
a
n
+
1
b
n
，
n
≤
10
，
2
c
n
-
10
，
n
＞
10
，
记数列{c_n}前n项和为T_n，求T₁₀₀．
组卷：28引用：2难度：0.5
解析
22．已知函数
f
（
x
）
=
x
-
1
x
+
1
+
alnx
（
a
∈
R
）
，g（x）=x-lnx+b（b∈R）．
（1）求函数f（x）的单调区间；
（2）设x₁，x₂是g（x）的两个零点，证明：x₁+x₂＞1-b.
组卷：19引用：2难度：0.6
解析