当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省无锡一中高二（上）质检数学试卷

发布：2024/9/11 5:0:9

一．单选题（每题5分，共40分）

1．直线
y
=
π
2
的倾斜角为（　　）
A．180° B．0° C．90° D．不存在
组卷：58引用：3难度：0.8
解析
2．已知直线l₁：ax+y+a=0与l₂：（a-6）x+（a-4）y-4=0，则“a=2”是“l₁∥l₂”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：184引用：7难度：0.8
解析
3．已知x+y=0，则
x
2
+
y
2
-
2
x
-
2
y
+
2
+
（
x
-
2
）
2
+
y
2
的最小值为（　　）
A．
5
B．2
2
C．
10
D．2
5
组卷：225引用：18难度：0.6
解析
4．已知点M（x₀，y₀）在圆x²+y²=2外，则直线x₀x+y₀y=2与圆的位置关系是（　　）
A．相切 B．相交 C．相离 D．不确定
组卷：169引用：5难度：0.5
解析
5．已知F₁，F₂是椭圆
x
2
25
+
y
2
16
=
1
的两个焦点，P是椭圆上一点，则|PF₁|•|PF₂|的最大值是（　　）
A．
25
4
B．9 C．16 D．25
组卷：1215引用：9难度：0.7
解析
6．瑞士数学家欧拉（Leonhard Euler）1765年在其所著的《三角形的几何学》一书中提出：任意三角形的外心、重心、垂心在同一条直线上．后人称这条直线为欧拉线．已知△ABC的顶点A（2，0），B（0，2），其欧拉线方程为2x-y-2=0，则顶点C的坐标是（　　）
A．（
18
5
，
16
5
） B．（
16
5
，
18
5
）
C．（
36
13
，
50
13
） D．（
50
13
，
36
13
）
组卷：90引用：7难度：0.7
解析
7．如图①，用一个平面去截圆锥得到的截口曲线是椭圆．许多人从纯几何的角度出发对这个问题进行过研究，其中比利时数学家Germinaldandelin（1794-1847）的方法非常巧妙，极具创造性．在圆锥内放两个大小不同的球，使得它们分别与圆锥的侧面、截面相切，两个球分别与截面相切于E、F，在截口曲线上任取一点A，过A作圆锥的母线，分别与两个球相切于C、B，由球和圆的几何性质，可以知道，AE=AC，AF=AB，于是AE+AF=AB+AC=BC．由B、C的产生方法可知，它们之间的距离BC是定值，由椭圆定义可知，截口曲线是以E、F为焦点的椭圆．

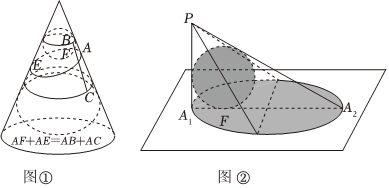
如图②，一个半径为2的球放在桌面上，桌面上方有一个点光源P，则球在桌面上的投影是椭圆，已知A₁A₂是椭圆的长轴，PA₁垂直于桌面且与球相切，PA₁=5，则椭圆的焦距为（　　）
A．4 B．6 C．8 D．12
组卷：167引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四．解答题（共70分）

21．在平面直角坐标系中，曲线E的轨迹方程为x²+y²=4．
（1）若直线l：y=kx-4与曲线E交于不同的两点C，D，且∠OCD=30°（O为坐标原点），求直线l的斜率；
（2）若点Q是直线l：x-y-4=0上的动点，过Q作曲线E的两条切线QM，QN，切点为M，N，探究：直线MN是否过定点．
组卷：47引用：3难度：0.5
解析
22．规定：在桌面上，用母球击打目标球，使目标球运动，球的位置是指球心的位置我们说球A是指该球的球心点A．两球碰撞后，目标球在两球的球心所确定的直线上运动，目标球的运动方向是指目标球被母球击打时，母球球心所指向目标球球心的方向．所有的球都简化为平面上半径为1的圆，且母球与目标球有公共点时，目标球就开始运动，在桌面上建立平面直角坐标系，解决下列问题：
（1）如图1，设母球A的位置为（0，0），目标球B的位置为（4，0），要使目标球B向C（8，-4）处运动，求母球A球心运动的直线方程；
（2）如图2，若母球A的位置为（0，-2），目标球B的位置为（4，0），能否让母球A击打目标B球后，使目标B球向（8，-4）处运动？
（3）若A的位置为（0，a）时，使得母球A击打目标球B时，目标球B（
4
2
，0）运动方向可以碰到目标球C（
7
2
，
-
5
2
），求a的最小值（只需要写出结果即可）．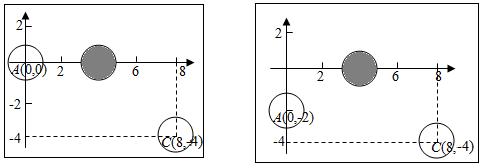
组卷：56引用：7难度：0.6
解析