2022-2023学年安徽师大附中高一（下）月考数学试卷（5月份）

一、单项选题：本大题共6小题，每小题4分，共24分，在每小题给出的四个选择项中，项是符合题目要求的.

• 1．在下列条件下，能确定一个平面的是（　　）

  A．空间的任意三点

  B．空间的任意一条直线和任意一点

  C．空间的任意两条直线

  D．梯形的两条腰所在的直线
  组卷：244引用：5难度：0.7

  解析

• 2．一个正方体内接于一个球，过球心作一个截面，则截面不可能的图形为（　　）

  A．

  B．

  C．

  D．
  组卷：421引用：9难度：0.9

  解析

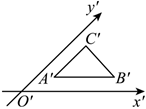• 3．如图，△A'B'C'是水平放置△ABC的直观图，其中B'C'=C'A'=1，A'B'∥x'轴，A'C'∥y'轴，则BC=（　　）

  A． 2

  B．2

  C． 6

  D．4
  组卷：145引用：7难度：0.7

  解析

• 4．圆台上、下底面积分别为36π和49π，母线长为5，则其轴截面面积为（　　）

  A． 13 6

  B． 26 6

  C． 13 2

  D． 26 2
  组卷：79引用：2难度：0.7

  解析

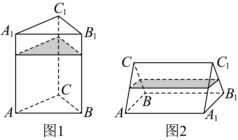• 5．如图1，一个正三棱柱容器，高为4，内装水若干，将容器放倒，把一个侧面作为底面，如图2，这时水面恰好是中截面，则图1中容器水面的高度是（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：52引用：4难度：0.5

  解析

• 6．棱长为

  2

  3

  的正四面体内切一球，然后在正四面体和该球形成的空隙处各放入一个小球，则这样一个小球的表面积最大为（　　）

  A． π 2

  B．π

  C． 2 π

  D． 3 π
  组卷：53引用：2难度：0.5

  解析

四、解答题：本题共5小题，共48分.请在答题卡指定区域作答，解答时应写出文字说明、证明过程或演算步骤.

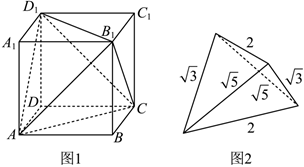• 17．为了求一个棱长为

  2

  的正四面体体积，小明同学设计如下解法：构造一个棱长为1的正方体，如图1：则四面体ACB₁D₁为棱长是

  2

  的正四面体，且有

  V

  四面体

  AC

  B

  1

  D

  1

  =

  V

  正方体

  -

  V

  B

  -

  AC

  B

  1

  -

  V

  A

  1

  -

  A

  B

  1

  D

  1

  -

  V

  C

  1

  -

  B

  1

  C

  D

  1

  -

  V

  D

  -

  AC

  D

  1

  =

  1

  3

  V

  正方体

  =

  1

  3

  ．
  学以致用：
  （1）如图2，一个四面体三组对棱长分别为

  3

  ，2，

  5

  ，求此四面体外接球表面积；
  （2）若四面体ABCD每组对棱长分别相等，求证：该四面体的四个面都是锐角三角形．
  组卷：10引用：2难度：0.5

  解析

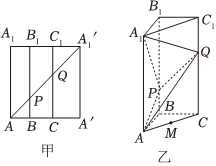• 18．如图甲所示的正方形AA'A'₁A₁中，AA₁=12，AB=A₁B₁=3，BC=B₁C₁=4，对角线AA'₁分别交BB₁，CC₁于点P，Q，将正方形AA'A'₁A₁沿BB₁CC₁折叠使得AA₁与A'A'₁重合，构成如图乙所示的三棱柱ABC-A₁B₁C₁．点M在棱AC上，且AM=

  15

  7

  ．
  （1）证明：BM∥平面APQ；
  （2）求三棱锥M-APQ的体积．
  组卷：202引用：4难度：0.6

  解析