当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省扬州中学教育集团树人学校七年级（上）第二次月考数学试卷

发布：2024/8/17 12:0:1

一、选择题（每题3分，共24分）

1．下列方程为一元一次方程的是（　　）
A．3x+2y=1 B．x²=1 C．x-1=0 D．y=x-1
组卷：192引用：4难度：0.8
解析
2．下列各数：-5，
π
3
，0，
22
7
，3.14，其中无理数有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：201引用：3难度：0.9
解析
3．2021年上半年，南京市的GDP总额达到了7622.8亿元，将7622.8亿用科学记数法表示为（　　）
A．7.6228×10¹² B．7.6228×10¹¹
C．0.76228×10¹² D．0.76228×10¹³
组卷：523引用：2难度：0.8
解析
4．《九章算术》是中国古代的一部数学专著，其中记载了一道有趣的题：“今有凫起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”大意是：今有野鸭从南海起飞，7天到北海；大雁从北海起飞，9天到南海．现野鸭从南海，大雁从北海同时起飞，问经过多少天相遇？设经过x天相遇，根据题意可列方程为（　　）
A．（9+7）x=1 B．（9-7）x=1 C．
（
1
7
-
1
9
）
x
=
1
D．
（
1
7
+
1
9
）
x
=
1
组卷：751引用：33难度：0.5
解析
5．某小组有m人，计划做n个“中国结”，若每人做5个，则可比计划多做9个；若每人做4个，则将比计划少做15个，现有下列四个方程：①5m+9=4m-15；②
n
+
9
5
=
n
+
15
4
③
n
+
9
5
=
n
-
15
4
；④5m-9=4m+15．其中正确的是（　　）
A．①② B．②④ C．②③ D．③④
组卷：992引用：4难度：0.7
解析
6．若有理数a、b满足等式|b-a|-|a+b|=2b,则有理数a、b在数轴上的位置可能是（　　）
A． B．
C． D．
组卷：1593引用：12难度：0.8
解析
7．长为300米的春游队伍，以2米/秒的速度向东行进．在排尾处的甲有一物品要送到排头，送到后立即返回排尾，甲的往返速度均为4米/秒．则往返共用的时间为（　　）
A．200s B．205s C．210s D．215s
组卷：764引用：5难度：0.6
解析
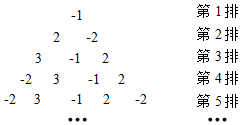8．将-1，2，-2，3按如图的方式排列，规定（m,n）表示第m排左起第n个数，则（5，4）与（21，7）表示的两个数之积是（　　）
A．-2 B．4 C．-4 D．6
组卷：620引用：2难度：0.7
解析

二、填空题（每题3分，共30分）

9．-3的相反数是
．
组卷：4968引用：350难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（共96分）

27．我们规定：对于数对（a,b），如果满足a+b=ab,那么就称数对（a,b）是“和积等数对”；如果满足a-b=ab,那么就称数对（a,b）是“差积等数对”，例如：
3
2
+
3
=
3
2
×3，2-
2
3
=
2
×
2
3
．所以数对（
3
2
，3）为“和积等数对”，数对（2，
2
3
）为“差积等数对”．
（1）下列数对中，“和积等数对”的是
；“差积等数对”的是
．
①（-
2
3
，-2），②（
2
3
，-2），③（
-
2
3
，2）．
（2）若数对（
x
-
1
2
，-2）是“差积等数对”，求x的值．
（3）是否存在非零有理数m,n,使数对（2m,n）是“和积等数对”，同时数对（2n,m）也是“差积等数对”，若存在，求出m,n的值，若不存在，说明理由．
组卷：955引用：7难度：0.5
解析
28．如图，线段AB=28厘米，点D和点C在线段AB上，且AC：BC=5：2，DC：AB=1：4．点P从点A出发以4厘米/秒的速度沿射线AD向点C运动，点P到达点C所在位置后立即按照原路原速返回，到达点D所在位置后停止运动，点Q从点B出发以1厘米/秒的速度沿着射线BC的方向运动，点Q到达点D所在的位置后停止运动．点P和点Q同时出发，点Q运动的时间为t秒．
（1）求线段AD的长度；
（2）当点C恰好为PQ的中点时，求t的值；
（3）当PQ=7厘米时，求t的值．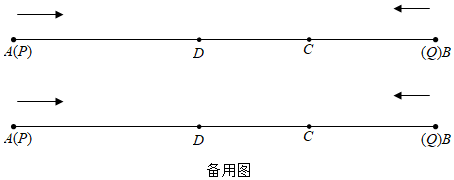
组卷：824引用：3难度：0.4
解析