2022-2023学年广西师大附中高二（上）期中数学试卷

一、单选题（8小题，共40.0分）

• 1．已知A（3，4，5），B（0，2，1），O（0，0，0），若

  OC

  =

  2

  5

  AB

  ，则C的坐标是（　　）

  A．（- 6 5 ，- 4 5 ，- 8 5 ）	B．（ 6 5 ，- 4 5 ，- 8 5 ）
  C．（- 6 5 ，- 4 5 ， 8 5 ）	D．（ 6 5 ， 4 5 ， 8 5 ）
  组卷：132引用：9难度：0.9

  解析

• 2．从甲地出发前往乙地，一天中有4趟汽车、3趟火车和1趟航班可供选择．某人某天要从甲地出发，去乙地旅游，则所有不同走法的种数是（　　）

  A．16

  B．15

  C．12

  D．8
  组卷：63引用：5难度：0.8

  解析

• 3．若点P到点（0，2）的距离比它到直线y=-1的距离大1，则点P的轨迹方程为（　　）

  A．y2=4x

  B．x2=4y

  C．y2=8x

  D．x2=8y
  组卷：1311引用：4难度：0.8

  解析

• 4．直线ax+y-a=0（a∈R）与圆（x-2）²+y²=4的位置关系是（　　）

  A．相离

  B．相交

  C．相切

  D．无法确定
  组卷：116引用：8难度：0.7

  解析

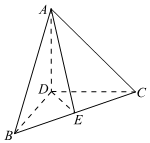• 5．如图，在三棱锥A-BCD中，DA，DB，DC两两垂直，且DB=DC，E为BC中点，则

  AE

  •

  BC

  等于（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：329引用：12难度：0.9

  解析

• 6．已知l₁：x+（m+1）y-2=0，l₂：mx+2y+4=0，则“m=1”是“l₁∥l₂”的（　　）条件．

  A．充分不必要	B．必要不充分
  C．充要条件	D．既不充分也不必要
  组卷：139引用：3难度：0.7

  解析

• 7．已知双曲线

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左焦点为F，右顶点为A，直线x=a与双曲线的一条渐近线的交点为B．若∠BFA=30°，则双曲线的离心率为（　　）

  A． 2

  B． 3

  C．2

  D．3
  组卷：199引用：7难度：0.8

  解析

四、解答题（本大题共6小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

• 21．图1是直角梯形ABCD，AB∥CD，∠D=90°，AB=2，DC=3，

  AD

  =

  3

  ，

  CE

  =

  2

  ED

  ，以BE为折痕将△BCE折起，使点C到达C₁的位置，且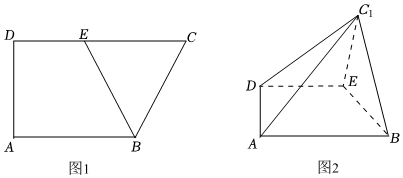

  A

  C

  1

  =

  6

  ，如图2．
  
  （1）求证：平面BC₁E⊥平面ABED；
  （2）在棱DC₁上是否存在点P，使得C₁到平面PBE的距离为

  6

  2

  ？若存在，求出二平面P-BE-A的大小；若不存在，说明理由．
  组卷：229引用：7难度：0.4

  解析

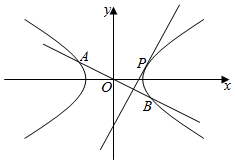• 22．在平面直角坐标系xOy中，已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的右焦点为（3，0），且经过点（2

  2

  ，1）．
  （1）求双曲线C的标准方程；
  （2）已知A，B是双曲线C上关于原点对称的两点，垂直于AB的直线l与双曲线C有且仅有一个公共点P，当点P位于第一象限，且△PAB被x轴分割为面积比为3：2的两部分时，求直线AB的方程．
  组卷：181引用：6难度：0.4

  解析