2022-2023学年江苏省常州二中高一(上)月考数学试卷(12月份)
发布:2024/9/27 22:0:1
一、单选择题:本题共8小题,每小题0分,共40分,在每小题给出的四个选项中,只有一项是符合要求的。
-
1.设a,b为实数,则“a<b”是“a2<b2”的( )
组卷:294引用:3难度:0.7 -
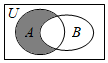 2.集合U=R,A={x|x2-x-2<0},B={x|y=},则图中阴影部分所表示的集合是( )11-x组卷:93引用:4难度:0.7
2.集合U=R,A={x|x2-x-2<0},B={x|y=},则图中阴影部分所表示的集合是( )11-x组卷:93引用:4难度:0.7 -
3.已知a=0.23,b=30.2,c=log0.23,则a,b,c的大小关系为( )
组卷:162引用:7难度:0.8 -
4.化简:
的结果是( )sin(3π-α)•cos(2π-α)•sin(32π-α)cos(π-α)•sin(-π-α)组卷:38引用:1难度:0.8 -
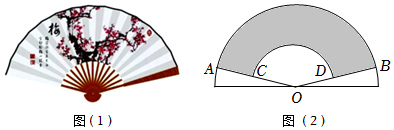 5.中国折叠扇有着深厚的文化底蕴如图(2),在半圆O中作出两个扇形OAB和OCD,用扇环形ABDC(图中阴影部分)制作折叠扇的扇面记扇环形ABDC的面积为S1,扇形OAB的面积为S2,当S1与S2的比值为时,扇面的形状较为美观,则此时弧5-12与弧ˆCD的长度之比为( )ˆAB组卷:301引用:5难度:0.7
5.中国折叠扇有着深厚的文化底蕴如图(2),在半圆O中作出两个扇形OAB和OCD,用扇环形ABDC(图中阴影部分)制作折叠扇的扇面记扇环形ABDC的面积为S1,扇形OAB的面积为S2,当S1与S2的比值为时,扇面的形状较为美观,则此时弧5-12与弧ˆCD的长度之比为( )ˆAB组卷:301引用:5难度:0.7 -
6.设函数f(x)=
,且x∈N*,若函数f(x)在其定义域上是单调递增函数,则实数a的取值范围是( )(4-a)x-5,x≤8ax-8,x>8组卷:22引用:1难度:0.5 -
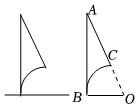 7.如图,某次帆船比赛LOGO的设计方案如下:在直角三角形ABO中挖去以点O为圆心,OB为半径的扇形BOC,使得扇形BOC的面积是直角三角形ABO面积的一半.记∠AOB=α,则的值为( )1-cos2α+sin2α2α•sinα•cosα组卷:11引用:1难度:0.7
7.如图,某次帆船比赛LOGO的设计方案如下:在直角三角形ABO中挖去以点O为圆心,OB为半径的扇形BOC,使得扇形BOC的面积是直角三角形ABO面积的一半.记∠AOB=α,则的值为( )1-cos2α+sin2α2α•sinα•cosα组卷:11引用:1难度:0.7
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
-
21.已知函数
.f(x)=(log216+log2x2)•log2x64
(1)求函数f(x)的值域;
(2)关于x的方程f(-x2+ax)=0恰有三个解,求实数a的取值集合;
(3)若f(x1)=f(x2)=m,且x2>2x1>0,求实数m的取值范围.组卷:213引用:6难度:0.6 -
22.定义:若对定义域内任意x,都有f(x+a)>f(x)(a为正常数),则称函数f(x)为“a距”增函数.
(1)若f(x)=2x-x,x∈(0,+∞),试判断f(x)是否为“1距”增函数,并说明理由;
(2)若,x∈R是“a距”增函数,求a的取值范围;f(x)=x3-14x+4
(3)若,x∈(-1,+∞),其中k∈R,且为“2距”增函数,求f(x)的最小值.f(x)=2x2+k|x|组卷:763引用:20难度:0.4


