当前位置：试卷中心 > 试卷详情

2023-2024学年重庆十八中高一（上）月考数学试卷（9月份）

发布：2024/9/5 0:0:8

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知集合A={x∈N|-1＜x＜3}，B={x|-2≤x＜2}，则A∩B=（　　）
A．{x|-1＜x＜2} B．{0，1} C．{1，2} D．{0，1，2}
组卷：130引用：11难度：0.7
解析
2．命题“∃x₀＞0，
x
2
0
-5x₀+6＞0”的否定是（　　）
A．∀x≤0，x²-5x+6≤0 B．∀x＞0，x²-5x+6≤0
C．∃x₀≤R，
x
2
0
-5x₀+6≤0 D．∃x₀＞0，
x
2
0
-5x₀+6≤0
组卷：189引用：20难度：0.7
解析
3．一个等腰三角形的底边长是6，腰长是一元二次方程x²-7x+12=0的一根，则此三角形的周长是（　　）
A．12 B．13 C．14 D．12或14
组卷：41引用：4难度：0.7
解析
4．二次函数y=ax²+bx+c（a,b,c为常数且a≠0）的图象如图所示，则一次函数y=ax+b与反比例函数
y
=
c
x
的图象可能是（　　）
A． B． C． D．
组卷：236引用：8难度：0.8
解析
5．在一个不透明的袋子里装有四个小球，球上分别标有6，7，8，9四个数字，这些小球除数字外都相同．甲、乙两人玩“猜数字”游戏，甲先从袋中任意摸出一个小球，将小球上的数字记为m,再由乙猜这个小球上的数字，记为n.如果m,n满足|m-n|≤1，那么就称甲、乙两人“心领神会”，则两人“心领神会”的概率是（　　）
A．
1
4
B．
3
8
C．
1
2
D．
5
8
组卷：52引用：3难度：0.7
解析
6．若
A
=
{
x
|
x
=
k
6
+
1
，
k
∈
Z
}
，
B
=
{
x
|
x
=
k
3
+
1
2
，
k
∈
Z
}
，
C
=
{
x
|
x
=
2
k
3
+
1
2
，
k
∈
Z
}
，则这三个集合间的关系是（　　）
A．A⊆B⊆C B．A⊆C⊆B C．C⊆B⊆A D．C⊆A⊆B
组卷：251引用：8难度：0.7
解析
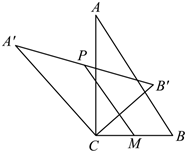7．如图，在Rt△ABC中，∠ACB=90°，将Rt△ABC绕顶点C逆时针旋转得到Rt△A′B′C′，M是BC的中点，P是A′B′的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值为（　　）
A．2.5 B．
2
+
3
C．3 D．4
组卷：81引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．（1）已知-1≤a+b≤1，-1≤a-b≤1，求2a+3b的取值范围；
（2）若实数a,b,c满足a²+b²+c²=6．试判断
1
a
2
+
1
+
1
b
2
+
2
与
1
2
-
1
c
2
+
3
的大小并说明理由．
组卷：137引用：3难度：0.5
解析
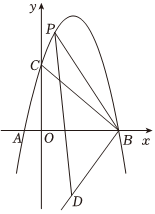22．如图，在平面直角坐标系中，抛物线y=ax²+bx+5（a≠0）与x轴交于点A（-1，0），B（5，0），与y轴交于点C．点D是抛物线对称轴上的一点，纵坐标为-5，P是线段BC上方抛物线上的一个动点，连接BP，DP．
（1）求抛物线的解析式；
（2）当△BDP的面积取最大值时，求点P的坐标和△BDP的面积的最大值；
（3）将抛物线y=ax²+bx+5（a≠0）沿着射线BD平移，使得新抛物线经过点D．新抛物线与x轴交于E，F两点（点E在点F左侧），与y轴交于点G，点M是新抛物线上的一动点，点N是坐标平面上一点，当以点E，G，M，N为顶点的四边形是矩形时，写出所有符合条件的点M的坐标，并写出求解点M的坐标的其中一种情况的过程．
组卷：8引用：1难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．∀x≤0，x²-5x+6≤0	B．∀x＞0，x²-5x+6≤0
C．∃x₀≤R， x 2 0 -5x₀+6≤0	D．∃x₀＞0， x 2 0 -5x₀+6≤0

2023-2024学年重庆十八中高一（上）月考数学试卷（9月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知集合A={x∈N|-1＜x＜3}，B={x|-2≤x＜2}，则A∩B=（ ）

2．命题“∃x0＞0，x20-5x0+6＞0”的否定是（ ）

3．一个等腰三角形的底边长是6，腰长是一元二次方程x2-7x+12=0的一根，则此三角形的周长是（ ）

4．二次函数y=ax2+bx+c（a,b,c为常数且a≠0）的图象如图所示，则一次函数y=ax+b与反比例函数y=cx的图象可能是（ ）

6．若A={x|x=k6+1，k∈Z}，B={x|x=k3+12，k∈Z}，C={x|x=2k3+12，k∈Z}，则这三个集合间的关系是（ ）

7．如图，在Rt△ABC中，∠ACB=90°，将Rt△ABC绕顶点C逆时针旋转得到Rt△A′B′C′，M是BC的中点，P是A′B′的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值为（ ）

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．（1）已知-1≤a+b≤1，-1≤a-b≤1，求2a+3b的取值范围；（2）若实数a,b,c满足a2+b2+c2=6．试判断1a2+1+1b2+2与12-1c2+3的大小并说明理由．

1．已知集合A={x∈N|-1＜x＜3}，B={x|-2≤x＜2}，则A∩B=（　　）

2．命题“∃x₀＞0，
x
2
0
-5x₀+6＞0”的否定是（　　）

3．一个等腰三角形的底边长是6，腰长是一元二次方程x²-7x+12=0的一根，则此三角形的周长是（　　）

4．二次函数y=ax²+bx+c（a,b,c为常数且a≠0）的图象如图所示，则一次函数y=ax+b与反比例函数
y
=
c
x
的图象可能是（　　）

6．若
A
=
{
x
|
x
=
k
6
+
1
，
k
∈
Z
}
，
B
=
{
x
|
x
=
k
3
+
1
2
，
k
∈
Z
}
，
C
=
{
x
|
x
=
2
k
3
+
1
2
，
k
∈
Z
}
，则这三个集合间的关系是（　　）

7．如图，在Rt△ABC中，∠ACB=90°，将Rt△ABC绕顶点C逆时针旋转得到Rt△A′B′C′，M是BC的中点，P是A′B′的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值为（　　）

21．（1）已知-1≤a+b≤1，-1≤a-b≤1，求2a+3b的取值范围；
（2）若实数a,b,c满足a²+b²+c²=6．试判断
1
a
2
+
1
+
1
b
2
+
2
与
1
2
-
1
c
2
+
3
的大小并说明理由．