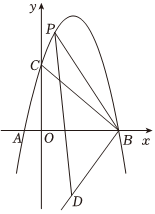
如图，在平面直角坐标系中，抛物线y=ax2+bx+5（a≠0）与x轴交于点A（-1，0），B（5，0），与y轴交于点C．点D是抛物线对称轴上的一点，纵坐标为-5，P是线段BC上方抛物线上的一个动点，连接BP，DP．
（1）求抛物线的解析式；
（2）当△BDP的面积取最大值时，求点P的坐标和△BDP的面积的最大值；
（3）将抛物线y=ax2+bx+5（a≠0）沿着射线BD平移，使得新抛物线经过点D．新抛物线与x轴交于E，F两点（点E在点F左侧），与y轴交于点G，点M是新抛物线上的一动点，点N是坐标平面上一点，当以点E，G，M，N为顶点的四边形是矩形时，写出所有符合条件的点M的坐标，并写出求解点M的坐标的其中一种情况的过程．
【考点】二次函数的性质与图象．
【答案】（1）y=-x2+4x+5；
（2）；
（3）（-1，4），（2，-5），（，），（，）．
（2）
529
24
（3）（-1，4），（2，-5），（
-
1
+
5
2
5
-
5
2
-
1
-
5
2
5
+
5
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/5 0:0:8组卷：8引用：1难度：0.5
