2022-2023学年上海市普陀区曹杨二中高二（下）月考数学试卷（3月份）

一、填空题（本大题共12题，满分54分，第1-6题每题4分，第7-12题每题5分）

• 1．圆x²+y²-2x-3=0的半径为

  ．
  组卷：159引用：5难度：0.9

  解析

• 2．若

  C

  2

  x

  -

  1

  8

  =

  C

  x

  +

  3

  8

  ，则实数x=

  ．
  组卷：63引用：1难度：0.8

  解析

• 3．已知某校高一（1）班有男生28人，女生21人，用分层抽样的方法从该班级中抽取若干人．已知某男生被抽中的概率为

  1

  7

  ，则抽取的女生人数为

  ．
  组卷：31引用：1难度：0.9

  解析

• 4．5位同学和2位老师一起拍照，要求排成一排，2位老师相邻但不排在两端，则不同的排法共有

  种．（结果用数字表示）
  组卷：86引用：1难度：0.6

  解析

• 5．若双曲线C的一条渐近线经过点（1，-2），且焦点到该渐近线的距离为2，则该双曲线的方程为

  ．
  组卷：279引用：3难度：0.7

  解析

• 6．对任意实数m,圆x²+y²-2mx-4my+6m-2=0恒过定点，则其坐标为

  ．
  组卷：317引用：3难度：0.7

  解析

• 7．在平面直角坐标系xOy中，已知△ABC顶点A（-4，0）和C（4，0），顶点B在椭圆

  x

  2

  25

  +

  y

  2

  9

  =

  1

  上，则

  sin

  A

  +

  sin

  C

  sin

  B

  =

  ．
  组卷：2853引用：55难度：0.7

  解析

三、解答题（本大题共5题，共78分）

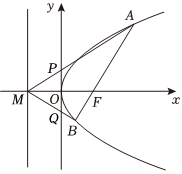• 20．如图，已知抛物线y²=4x的焦点为F，准线与x轴的交点为M．过点F的直线与抛物线交于A、B两点．
  （1）若点A在第一象限，且|AF|=4，求直线AB的倾斜角；
  （2）若点M在以线段AB为直径的圆周上，求直线AB的方程；
  （3）设直线AM、BM分别与y轴交于P、Q两点，记△MAB、△MPQ的面积分别为S₁、S₂，求

  S

  1

  S

  2

  的取值范围．
  组卷：71引用：1难度：0.3

  解析

• 21．已知椭圆T：

  x

  2

  2

  +

  y

  2

  =

  1

  ，F₁，F₂是左右焦点，且直线l过点p（m,0）（

  m

  ＜

  -

  2

  ）交椭圆T于A，B两点，点A，B在x轴上方，点A在线段BP上．
  （1）若B为上顶点，

  |

  B

  F

  1

  |

  =

  |

  P

  F

  1

  |

  ，求m的值；
  （2）若

  F

  1

  A

  •

  F

  2

  A

  =

  1

  3

  ，原点O到直线l的距离为

  4

  15

  15

  ，求直线l的方程；
  （3）对于任意点P，是否存在唯一的直线l,使得

  F

  1

  A

  ∥

  F

  2

  B

  ，若存在，求出直线l的斜率，若不存在，请说明理由．
  组卷：53引用：3难度：0.5

  解析