2023-2024学年湖南省长沙市雅礼中学高二（上）入学数学试卷
发布：2024/8/3 8:0:9
一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．已知复数z=（1-i）+λ（1+i）是纯虚数，则实数λ=（ ）
组卷：46引用：5难度：0.8 -
2．已知集合A={（x,y）|x=y}，B={（x,y）|y=8-x}，则A∩B=（ ）
组卷：135引用：5难度：0.8 -
3．已知x∈R，则x≥1且y≥4是x+y≥5且xy≥4成立的（ ）
组卷：205引用：3难度：0.9 -
4．有一个人在打靶中，连续射击2次，事件“至少有1次中靶”的对立事件是（ ）
组卷：912引用：32难度：0.9 -
5．已知样本数据x1，x2，…，x2022的平均数和方差分别为3和56，若yi=2xi+3（i=1，2，…，2022），则y1，y2，…，y2022的平均数和方差分别是（ ）
组卷：348引用：4难度：0.9 -
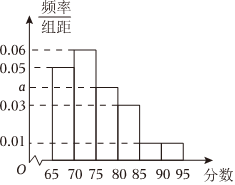6．某中学举行了一次“网络信息安全”知识竞赛，将参赛的100名学生成绩分为6组，绘制了如图所示的频率分布直方图，则成绩在区间[75，80）内的学生有（ ）组卷：137引用：4难度：0.7 -
7．已知函数f（x）的定义域为R，且f（x+y）+f（x-y）=f（x）f（y），f（1）=1，则
f（k）=（ ）22∑k=1组卷：5948引用：15难度：0.5
四、解答题（本题共6小题，共70分，其中第17题10分，其它每题12分，解答应写出文字说明、证明过程或演算步骤.）
-
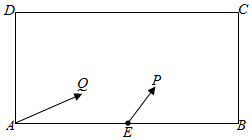21．某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛，在E处按方向释放机器人甲，同时在A处按EP方向释放机器人乙，设机器人乙在M处成功拦截机器人甲，两机器人停止运动．若点M在矩形区域ABCD内（包含边界），则挑战成功，否则挑战失败．已知AB=6米，E为AB中点，比赛中两机器人均匀速直线运动方式行进，记AQ与EP的夹角为θ（0＜θ＜π），EB与AQ的夹角为α（AB）．0＜α＜π2
（1）若两机器人运动方向的夹角为，AD足够长，机器人乙挑战成功，求两机器人运动路程和的最大值；π3
（2）已知机器人乙的速度是机器人甲的速度的2倍．
（ⅰ）若，AD足够长，机器人乙挑战成功，求sinα．θ=π3
（ⅱ）如何设计矩形区域ABCD的宽AD的长度，才能确保无论θ的值为多少，总可以通过设置机器人乙的释放角度α使机器人乙挑战成功？组卷：85引用：8难度：0.6 -
22．定义：
，为实数θ1，θ2，⋯，θn对θ0的“正弦方差”．μ=1n[sin2（θ1-θ0）+sin2（θ2-θ0）+⋯+sin2（θn-θ0）]
（1）若，证明：实数θ1，θ2，θ3对θ0的“正弦方差”μ的值是与θ0无关的定值；θ1=π3，θ2=2π3，θ3=π
（2）若，若实数θ1，θ2，θ3对θ0的“正弦方差”μ的值是与θ0无关的定值，求α，β值．θ1=π4，θ2=α，θ3=β，α∈（π2，π），β∈（π，2π）组卷：424引用：3难度：0.3
