当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省盐城市东台市第五教育联盟九年级（上）第一次质检数学试卷（10月份）

发布：2024/9/16 15:0:8

一、选择题（本大题共8小题，每小题3分，共24分）

1．用配方法解方程x²+8x+9=0，变形后的结果正确的是（　　）
A．（x+4）²=-7 B．（x+4）²=-9 C．（x+4）²=7 D．（x+4）²=25
组卷：2099引用：158难度：0.7
解析
2．下列方程中，有一个根为-1的方程是（　　）
A．x²-x=0 B．x²-7x+6=0 C．2x²-3x-5=0 D．3x²+2x-5=0
组卷：77引用：5难度：0.7
解析
3．方程x²-2=0的两个根为（　　）
A．x₁=x₂=2 B．x₁=2，x₂=-2 C．x₁=x₂=
2
D．x₁=
2
，x₂=-
2
组卷：49引用：5难度：0.9
解析
4．下列方程中，是关于x的一元二次方程的是（　　）
A．
1
x
2
-
x
-
1
=
0
B．ax²+bx+c=0（a、b、c为常数）
C．（x+1）（x-2）=x²
D．3x²+1=0
组卷：742引用：11难度：0.8
解析
5．若⊙O的半径为5cm,点A到圆心O的距离为6cm,那么点A与⊙O的位置关系是（　　）
A．点A在圆外 B．点A在圆上 C．点A在圆内 D．不能确定
组卷：347引用：8难度：0.9
解析
6．如图，AB是⨀O的直径，
ˆ
AC
=3
ˆ
BC
，则∠BAC=（　　）
A．67.5° B．45° C．30° D．22.5°
组卷：565引用：6难度：0.8
解析
7．如图，点A、B、C在⊙O上，若∠C=38°，则∠AOB的度数为（　　）
A．38° B．76° C．80° D．60°
组卷：753引用：13难度：0.9
解析
8．点C是以AB为直径的半圆O上的动点，D在BC上，且BD=2CD，点E、F、G分别是AC、DE、AD的中点．若AB=12，则△OFG的面积最大值为（　　）
A．2 B．3 C．6 D．9
组卷：279引用：2难度：0.4
解析

二、填空题（本大题共8小题，每小题3分，共24分）

9．若关于x的方程（a-1）x²+4x-3=0是一元二次方程，则a的取值范围是
．
组卷：585引用：9难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共11小题，共102分．解答应写出文字说明、证明过程或演算步骤．）

26．教育部印发《义务教育课程方案》和课程标准（2022年版），将劳动从原来的综合实践活动课程中独立出来．某中学为了让学生体验农耕劳动，如图（1）在正方形绿化带ABCD内修建一个矩形耕种园AEFG，其中点G在AD上，点E在AB上，已知正方形绿化带ABCD的面积为400m²，AB，AD是墙壁，BC、CD无墙壁．已知矩形耕种园AEFG的面积为正方形花园面积的
1
4
，该耕种园借助绿化带的墙壁，只设置围栏GF、EF即可．小明用所学的数学知识进行了如下探究．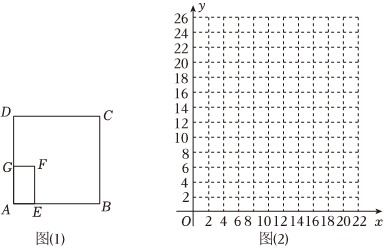

（1）建立数学模型由题意知，此耕种园的面积为
400
×
1
4
=
100
（
m
2
）
，设AE=x米，则
AG
=
100
x
米．设所需围栏的长度为y米，则y关于x的函数解析式为
；
（2）画出函数图象：

x 5 8 10 12.5 16 20

y 25 20.5 20 20.5 22.25 a

①列表：其中，a=
；
②请根据上表数据，在如图（2）所示的平面直角坐标系中描点，并画出y关于x的函数图象，其中，自变量x的取值范围是
；
（3）观察函数图象，解决问题：
①当所用围栏20米时，求AE的长；
②若围栏的长度为b米，则b的取值范围为
时，每一个b值都对应两种围栏方式．
组卷：114引用：1难度：0.2
解析
27．【阅读材料】如图1所示，对于平面内⊙P，在⊙P上有弦AB，取弦AB的中点M，我们把弦AB的中点M到某点或某直线的距离叫做弦AB到这点或者这条直线的“密距”．例如：图1中线段MO的长度即为弦AB到原点O的“密距”，过点M作y轴的垂线交y轴于点N，线段MN的长度即为弦AB到y轴的“密距”．
【类比应用】已知⊙P的圆心为P（0，8），半径为4，弦AB的长度为4，弦AB的中点为M．
（1）当AB∥y轴时，如图2所示，圆心P到弦AB的中点M的距离是
，此时弦AB到原点O的“密距”是
．
（2）①如果弦AB在⊙P上运动，在运动过程中，圆心P到弦AB的中点M的距离变化吗？若不变化，请求出PM的长，若变化，请说明理由．
②直接写出弦AB到原点的“密距”d的取值范围
；
【拓展应用】如图3所示，已知⊙P的圆心为P（0，8），半径为4，点A（0，4），点B为⊙P上的一动点，弦AB到直线y=-x-6的“密距”的最大值是
（直接写出答案）．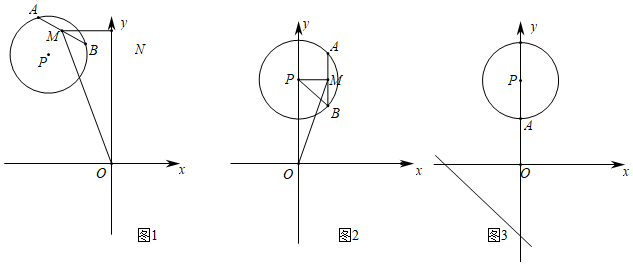
组卷：198引用：3难度：0.2
解析