教育部印发《义务教育课程方案》和课程标准（2022年版），将劳动从原来的综合实践活动课程中独立出来．某中学为了让学生体验农耕劳动，如图（1）在正方形绿化带ABCD内修建一个矩形耕种园AEFG，其中点G在AD上，点E在AB上，已知正方形绿化带ABCD的面积为400m2，AB，AD是墙壁，BC、CD无墙壁．已知矩形耕种园AEFG的面积为正方形花园面积的14，该耕种园借助绿化带的墙壁，只设置围栏GF、EF即可．小明用所学的数学知识进行了如下探究．
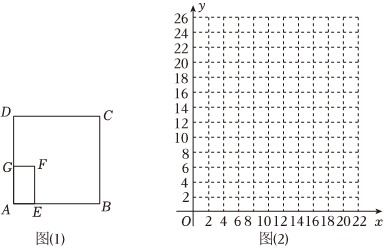
（1）建立数学模型由题意知，此耕种园的面积为400×14=100（m2），设AE=x米，则AG=100x米．设所需围栏的长度为y米，则y关于x的函数解析式为 y=100x+xy=100x+x；
（2）画出函数图象：
1
4
400
×
1
4
=
100
（
m
2
）
AG
=
100
x
y
=
100
x
+
x
y
=
100
x
+
x
| x | 5 | 8 | 10 | 12.5 | 16 | 20 |
| y | 25 | 20.5 | 20 | 20.5 | 22.25 | a |
25
25
；②请根据上表数据，在如图（2）所示的平面直角坐标系中描点，并画出y关于x的函数图象，其中，自变量x的取值范围是
5≤x≤20
5≤x≤20
；（3）观察函数图象，解决问题：
①当所用围栏20米时，求AE的长；
②若围栏的长度为b米，则b的取值范围为
20＜b≤25
20＜b≤25
时，每一个b值都对应两种围栏方式．【考点】四边形综合题．
【答案】；25；5≤x≤20；20＜b≤25
y
=
100
x
+
x
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/16 15:0:8组卷：114引用：1难度：0.2
相似题
-
1．在四边形ABCD中，AB=BC，∠B=90°；
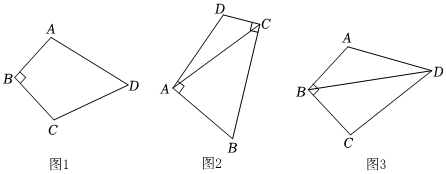
（1）如图1，已知∠D=60°，则∠A+∠C的度数等于 °；
（2）如图2，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC．若AC=6，求四边形ABCD的面积；
（3）如图3，已知AB=BC，∠ADC=60°，∠B=90°，AD=4，CD=4，求线段BD的长度．3发布：2025/5/24 3:30:1组卷：199引用：1难度：0.5 -
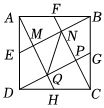2．如图，点E，F，G，H分别是正方形ABCD的边DA，AB，BC，CD的中点，连接AH，BE，CF，DG，它们分别相交于点M，N，P，Q，连接NQ．若AB=4，则下列结论错误的是（ ）发布：2025/5/24 4:0:7组卷：148引用：1难度：0.2 -
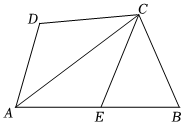3．如图，在四边形ABCD中，AD=11，BC=CD=13，对角线AC=20，点E是AB边上一点，连接CE．
（1）若AB＞AD且AC平分∠DAB，
①当AE=AD时，求证：CE=BC；
②求线段CE的最小值；
（2）当点E是AB边的中点，且CE=BC时，直接写出△ABC的面积．12发布：2025/5/24 3:0:1组卷：152引用：1难度：0.4
