2022-2023学年湖南省怀化市、长沙市高三（上）开学数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={x|a-2＜x＜a+3}，B={x|（x-1）（x-4）＞0}，若A∪B=R，则a的取值范围是（　　）

  A．（-∞，1]

  B．（1，3）

  C．[1，3]

  D．[3，+∞）
  组卷：119引用：7难度：0.8

  解析

• 2．设i是虚数单位，已知复数z满足（1-i）z=1+（a-1）i（a∈R），且复数z是纯虚数，则实数a=（　　）

  A． - 1 2

  B． 1 2

  C．1

  D．2
  组卷：37引用：3难度：0.7

  解析

• 3．已知函数f（x）=e^x-1+ax²+1的图象在x=1处的切线与直线x+3y-1=0垂直，则实数a的值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：564引用：4难度：0.9

  解析

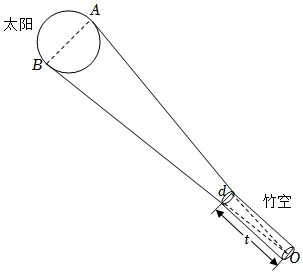• 4．《周髀算经》中“侧影探日行”一文有记载：“即取竹空，径一寸，长八尺，捕影而视之，空正掩目，而日应空之孔．”意谓：“取竹空这一望筒，当望筒直径d是一寸，筒长l是八尺时（注：一尺等于十寸），从筒中搜捕太阳的边缘观察，则筒的内孔正好覆盖太阳，而太阳的外缘恰好填满竹管的内孔．”如图所示，O为竹空底面圆心，则太阳角∠AOB的正切值为（　　）

  A． 320 160 2 - 1

  B． 1 160

  C． 160 80 2 - 1

  D． 1 80
  组卷：566引用：12难度：0.5

  解析

• 5．将函数f（x）=2cos（x-φ）图像上各点的横坐标变为原来的ω（ω＞0）倍，纵坐标不变，得到函数g（x）的图像，若对于满足|g（x₁）-g（x₂）|=4的x₁，x₂，都有|x₁-x₂|_min=

  π

  4

  ，则ω的值为（　　）

  A． 1 4

  B． 1 2

  C．2

  D．4
  组卷：13引用：3难度：0.7

  解析

• 6．已知抛物线C：y²=2px（p＞0）的焦点为F，点

  M

  （

  x

  0

  ，

  10

  ）

  （

  x

  0

  ＞

  p

  2

  ）

  是抛物线C上一点，圆M与线段MF相交于点A，且被直线

  x

  =

  p

  2

  截得的弦长为

  3

  |

  MA

  |

  ，若|MA|=2|AF|，则|AF|=（　　）

  A．2

  B．1

  C． 5 2

  D． 5
  组卷：15引用：3难度：0.5

  解析

• 7．已知三棱锥P-ABC，Q为BC中点，PB=PC=AB=BC=AC=2，侧面PBC⊥底面ABC，则过点Q的平面截该三棱锥外接球所得截面面积的取值范围为（　　）

  A． [ π ， 5 π 3 ]

  B． [ π 2 ， 2 π 3 ]

  C． [ 2 π 3 ， 2 π ]

  D．[π，2π]
  组卷：629引用：5难度：0.3

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤。

• 21．已知椭圆

  Γ

  ：

  x

  2

  a

  2

  +

  y

  2

  =

  1

  ，（a＞1）的上、下顶点是B₁，B₂，左，右顶点是A₁，A₂，点D在椭圆Γ内，点M在椭圆Γ上，在四边形MB₁DB₂中，若MB₁⊥B₁D，MB₂⊥B₂D，且四边形MB₁DB₂面积的最大值为

  5

  2

  ．
  （1）求a的值；
  （2）已知直线x=my+1交椭圆Γ于P，Q两点，直线A₁P与A₂Q交于点S，证明：当m变化时，存在不同于A₂的定点T，使得|A₂S|=|ST|．
  组卷：21引用：2难度：0.3

  解析

• 22．已知函数f（x）=e^x+2ax-1，其中a为实数，e为自然对数底数，e=2.71828…．
  （1）已知函数x∈R，f（x）＞0，求实数a取值的集合；
  （2）已知函数F（x）=f（x）-ax²有两个不同极值点x₁、x₂．
  ①求实数a的取值范围；
  ②证明：2

  a

  （

  x

  1

  +

  x

  2

  ）

  ＞

  3

  x

  1

  x

  2

  ．
  组卷：42引用：3难度：0.2

  解析