2022-2023学年湖南省长沙一中高二（下）第二次段考数学试卷

一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知全集U=R，若A={x∈N|0＜x≤6}，B={x|-x²+3x+4≤0}，则A∩（∁_UB）=（　　）

  A．（0，4]

  B．（0，1]

  C．{1}

  D．{1，2，3}
  组卷：225引用：5难度：0.8

  解析

• 2．设复数

  z

  =

  1

  +

  i

  3

  2

  -

  i

  ，则z的虚部是（　　）

  A． - 1 5 i

  B． - 1 5

  C． 3 5 i

  D． 3 5
  组卷：30引用：1难度：0.9

  解析

• 3．设a,b为正实数，且a+b=10ab,则a+9b的最小值为（　　）

  A． 6 5

  B． 13 10

  C． 8 5

  D． 9 5
  组卷：1873引用：5难度：0.8

  解析

• 4．函数

  f

  （

  x

  ）

  =

  x

  2

  e

  x

  的大致图像为（　　）

  A．

  B．

  C．

  D．
  组卷：347引用：14难度：0.7

  解析

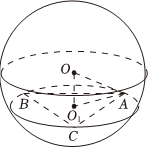• 5．已知A，B，C为球O的球面上的三个点，⊙O₁为△ABC的外接圆，若⊙O₁的面积为π，AB=BC=AC=

  3

  O

  O

  1

  ，则球O的表面积为（　　）

  A．4π

  B．8π

  C．12π

  D．16π
  组卷：74引用：2难度：0.5

  解析

• 6．已知抛物线C：y²=2x的焦点为F，A（x₁，y₁），B（x₂，y₂）是C上两点，若

  y

  2

  2

  -2

  y

  2

  1

  =1，则

  |

  BF

  |

  |

  AF

  |

  =（　　）

  A． 1 2

  B． 2 2

  C． 2

  D．2
  组卷：64引用：1难度：0.6

  解析

• 7．以罗尔中值定理、拉格朗日中值定理、柯西中值定理为主体的“中值定理”反映了函数与导数之间的重要联系，是微积分学重要的理论基础，其中拉格朗日中值定理是“中值定理”的核心内容，其定理陈述如下：如果函数f（x）在区间[a,b]上的图象是一条连续不断的曲线，且在开区间（a,b）内存在导函数，则在区间（a,b）内至少存在一个点x₀∈（a,b），使得f'（x₀）=

  f

  （

  b

  ）

  -

  f

  （

  a

  ）

  b

  -

  a

  ，

  x

  =

  x

  0

  称为函数y=f（x）在区间[a,b]上的中值点．若关于函数f（x）=e^x在区间[0，1]上“中值点”个数为m,函数g（x）=sinx+

  3

  cosx在区间[0，π]上“中值点”的个数为n,则（　　）

  A．m=0，n=1

  B．m=1，n=1

  C．m=1，n=2

  D．m=2，n=1
  组卷：47引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

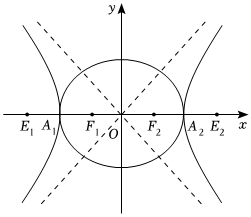• 21．如图，椭圆Γ₁、双曲线Γ₂中心为坐标原点O，焦点在x轴上，且有相同的顶点A₁，A₂，Γ₁的焦点为F₁，F₂，Γ₂的焦点为E₁，E₂，点A₁，F₁，O，F₂，A₂恰为线段E₁E₂的六等分点，我们把Γ₁和Γ₂合成为曲线Γ，已知Γ₁的长轴长为4．
  （1）求曲线Γ的方程；
  （2）若M为Γ上一动点，T（0，4）为定点，求|MT|的最小值；
  （3）若直线l过点O，与Γ₁交于P₁，P₂两点，与Γ₂交于Q₁，Q₂两点，点P₁、Q₁位于同一象限，且直线P₁F₁∥Q₁E₁，求直线l的方程．
  组卷：62引用：4难度：0.3

  解析

• 22．已知函数f（x）=（x+a）e^x，a∈R．
  （1）讨论f（x）在（0，+∞）的单调性；
  （2）是否存在a,x₀，x₁，且x₀≠x₁，使得曲线y=f（x）在x=x₀和x=x₁处有相同的切线？证明你的结论．
  组卷：201引用：3难度：0.4

  解析