2022-2023学年山东省滨州市六校联考高二（下）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．从甲、乙、丙3幅不同的画中选出2幅，送给甲、乙两人，则共有（　　）种不同的送法．

  A．6

  B．5

  C．3

  D．2
  组卷：25引用：4难度：0.7

  解析

• 2．某人翻开电话本给自己的一位朋友打电话时，发现电话号码的最后一位数字变得模糊不清了，因此决定随机拨号进行尝试，那么该人尝试两次但都拨不对电话号码的概率为（　　）

  A． 81 100

  B． 18 25

  C． 4 5

  D． 3 5
  组卷：47引用：4难度：0.7

  解析

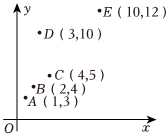• 3．有一散点图如图所示，在5个数据（x,y）中去掉D（3，10）后，下列说法正确的是（　　）

  A．相关系数r变小

  B．残差平方和变小

  C．变量x,y负相关

  D．解释变量x与预报变量y的相关性变弱
  组卷：36引用：7难度：0.7

  解析

• 4．已知随机变量X服从参数为0.3的两点分布，若Y=2X+1，E（Y）=（　　）

  A．0.3

  B．0.7

  C．1.6

  D．2.4
  组卷：77引用：4难度：0.7

  解析

• 5．若x⁴+（x+1）⁷=a₀+a₁（x+2）+a₂（x+2）²+…+a₇（x+2）⁷，则a₃=（　　）

  A．-8

  B．35

  C．-43

  D．27
  组卷：387引用：4难度：0.6

  解析

• 6．甲、乙两选手进行乒乓球比赛的初赛，已知每局比赛甲获胜的概率是0.4，乙获胜的概率是0.6，若初赛采取三局两胜制，则乙最终获胜的概率是（　　）

  A．0.144

  B．0.352

  C．0.432

  D．0.648
  组卷：176引用：5难度：0.5

  解析

• 7．小李的手机购物平台经常出现她喜欢的商品，这是电商平台推送的结果．假设电商平台第一次给小李推送某商品时，她购买此商品的概率为

  3

  4

  ；从第二次推送起，若前一次不购买此商品，则此次购买的概率为

  1

  3

  ；若前一次购买了此商品，则此次仍购买的概率为

  2

  5

  ，那么电商平台在第2次推送时小李不购买此商品的概率为（　　）

  A． 37 60

  B． 3 5

  C． 1 6

  D． 9 20
  组卷：156引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．某学校高一年级上学期有3次英语素养测评，测评结果为一等奖和二等奖，已知甲同学每次测评获一等奖的概率为

  1

  3

  ，乙同学每次测评获一等奖的概率为

  1

  2

  ．
  （1）求甲同学在3次测评中恰有1次获得一等奖且第2次测评未获得一等奖的概率；
  （2）由于客观因素，这个学期第一次测评成绩作废，后两次成绩作为评价学生的依据．每次测评获得一等奖记5分，二等奖记3分，甲同学英语素养测评得分为X，乙同学得分为Y，设随机变量ξ=X-Y，求ξ的分布列与期望．
  组卷：46引用：2难度：0.5

  解析

• 22．某中学以学生为主体，以学生的兴趣为导向，注重培育学生广泛的兴趣爱好，开展了丰富多彩的社团活动，其中一项社团活动为《奇妙的化学》，注重培养学生的创新精神和实践能力．本社团在选拔赛阶段，共设两轮比赛．第一轮是实验操作，第二轮是基础知识抢答赛．第一轮给每个小组提供5个实验操作的题目，小组代表从中抽取2个题目，若每个题目的实验流程操作规范可得10分，否则得0分．
  （1）已知某小组会5个实验操作题目中的3个，求该小组在第一轮得20分的概率；
  （2）已知恰有甲、乙、丙、丁四个小组参加化学基础知识的抢答比赛，每一次由四个小组中的一个回答问题，无论答题对错，该小组回答后由其他小组抢答下一问题，且其他小组有相同的机会抢答下一问题．记第n次回答的是甲的概率是P_n，若P₁=1．
  ①求P₃和P₄；
  ②写出P_n与P_n-1之间的关系式，并比较第9次回答的是甲和第10次回答的是甲的可能性的大小．
  组卷：69引用：3难度：0.5

  解析