当前位置：试卷中心 > 试卷详情

2022-2023学年重庆市铜梁中学、江津中学等七校联考高二（下）期末数学试卷

发布：2024/5/30 8:0:9

1．已知集合A={x|y=x,x∈R}，B={y|y=lnx,x＞1}，则A∩B=（　　）
A．∅ B．{（1，1）} C．（0，+∞） D．R
组卷：45引用：1难度：0.8
解析
2．已知命题p：∃x₀∈R，x₀=-2或x₀=3，则（　　）
A．￢p：∀x∈R，x≠-2或x≠3 B．￢p：∀x∈R，x≠-2且x≠3
C．￢p：∀x∈R，x=-2且x=3 D．￢p：∃x₀∉R，x₀=-2或x₀=3
组卷：169引用：1难度：0.8
解析
3．
（
2
x
+
1
）
4
=
a
4
x
4
+
a
3
x
3
+
a
2
x
2
+
a
1
x
+
a
0
，则a₀+a₂+a₄=（　　）
A．41 B．40 C．-40 D．-41
组卷：253引用：3难度：0.7
解析
4．已知函数y=f（x+1）定义域是[-2，3]，则y=f（2x-1）的定义域是（　　）
A．
[
0
，
5
2
]
B．[-1，4] C．[-5，5] D．[-3，7]
组卷：3359引用：73难度：0.9
解析
5．函数
y
=
sinx
•
2
x
+
1
2
x
-
1
的部分图象大致为（　　）
A． B． C． D．
组卷：51引用：5难度：0.7
解析
6．已知函数
y
=
（
1
-
a
）
x
+
14
a
,
x
＜
10
lgx
,
x
≥
10
的值域为R，则实数a的取值范围是（　　）
A．（-∞，1） B．[-
9
4
，+∞） C．[-
9
4
，1） D．（-
9
4
，1）
组卷：606引用：2难度：0.6
解析
7．已知函数f（x）=x²-4x-alnx,则f（x）在（1，3）上不单调的一个充分不必要条件是（　　）
A．a∈（-∞，-2） B．a∈（6，+∞） C．a∈（-2，0） D．a∈（-2，6）
组卷：98引用：3难度：0.7
解析

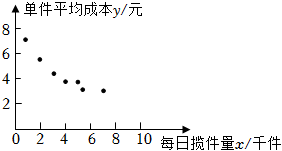21．快递业的迅速发展导致行业内竞争日趋激烈．某快递网点需了解一天中收发一件快递的平均成本y（单位：元）与当天揽收的快递件数即揽件量x（单位：千件）之间的关系，对该网点近7天的每日揽件量x_i（单位：千件）与当日收发一件快递的平均成本y_i（单位：元）（i=1，2，3，4，5，6，7）的数据进行了初步处理，得到散点图及一些统计量的值．

x

y

w

7
∑
i
=
1
（
x
i
-
x
）
（
y
i
-
y
）

7
∑
i
=
1
（
w
i
-
w
）
（
y
i
-
y
）

7
∑
i
=
1
（
x
i
-
x
）
2

7
∑
i
=
1
（
w
i
-
w
）
2

4 4.6 0.37 -18 2.75 25.5 0.55

表中
w
i
=
1
x
i
，
w
=
1
7
7
∑
i
=
1
w
i
．
（1）根据散点图判断y=ax+b与
y
=
c
+
d
x
哪一个更适宜作为y关于x的经验回归方程类型？并根据判断结果及表中数据求出y关于x的经验回归方程；
（2）已知该网点每天的揽件量x（单位：千件）与单件快递的平均价格t（单位：元）之间的关系是
x
=
59
-
4
t
（
5
.
75
≤
t
≤
14
.
5
）
，收发一件快递的利润等于单件的平均价格减去平均成本，根据（1）中建立的经验回归方程解决以下问题：
①预测该网点某天揽件量为2千件时可获得的总利润；
②单件快递的平均价格t为何值时，该网点一天内收发快递所获利润的预报值最大？
附：对于一组具有线性相关关系的数据（μ_i，v_i）（i=1，2，⋯，n），其经验回归直线
̂
v
=
̂
β
μ
+
̂
α
的斜率和截距的最小二乘估计分别为
̂
β
=
n
∑
i
=
1
（
μ
i
-
μ
）
（
v
i
-
v
）
n
∑
i
=
1
（
μ
i
-
μ
）
2
，
̂
α
=
v
-
̂
β
μ
．

组卷：70引用：2难度：0.6

A．￢p：∀x∈R，x≠-2或x≠3	B．￢p：∀x∈R，x≠-2且x≠3
C．￢p：∀x∈R，x=-2且x=3	D．￢p：∃x₀∉R，x₀=-2或x₀=3

x	y	w	7 ∑ i = 1 （ x i - x ）（ y i - y ）	7 ∑ i = 1 （ w i - w ）（ y i - y ）	7 ∑ i = 1 （ x i - x ） 2	7 ∑ i = 1 （ w i - w ） 2
4	4.6	0.37	-18	2.75	25.5	0.55