2023-2024学年浙江省台州市玉环市玉城中学高一（上）入学数学试卷

一．选择题（10×3′，共30分）

• 1．下列计算正确的是（　　）

  A．x2+x3=x5

  B．x3•x2=x6

  C．（x2）3=x6

  D．（2x）3=6x3
  组卷：62引用：1难度：0.8

  解析

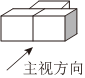• 2．三个大小一样的正方体按如图摆放，它的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：23引用：1难度：0.8

  解析

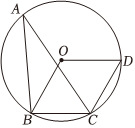• 3．如图，点A，B，C，D均在以点O为圆心的圆O上，连接AB，AC及顺次连接O，B，C，D得到四边形OBCD，若OD=BC，OB=CD，则∠A的度数为（　　）​

  A．20°

  B．25°

  C．30°

  D．35°
  组卷：3引用：1难度：0.7

  解析

• 4．如果a＜b＜0，那么下列式子中一定成立的是（　　）

  A．a2＞ab

  B．a2＜b2

  C． a b ＜ 1

  D． 1 a ＜ 1 b
  组卷：448引用：9难度：0.7

  解析

• 5．已知集合U={-2，-1，0，1，2，3}，A={1，2}，B={-1，0，1}，则∁_U（A∪B）=（　　）

  A．{-2，3}	B．{-2，2，3}
  C．{-2，-1，0，3}	D．{-2，-1，0，2，3}
  组卷：163引用：8难度：0.7

  解析

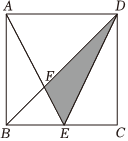• 6．如图，在正方形ABCD中，E是BC的中点，△DEF的面积等于3，则此正方形ABCD的面积等于（　　）​

  A．6

  B．12

  C．16

  D．18
  组卷：6引用：1难度：0.6

  解析

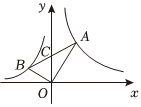• 7．如图，Rt△AOB的直角顶点O为坐标原点，点A在反比例函数

  y

  =

  3

  x

  （

  x

  ＞

  0

  ）

  的图象上，点B在反比例函数

  y

  =

  k

  x

  （

  x

  ＜

  0

  ）

  的图象上，AB交y轴于点C，∠OAB=30°，则k的值为（　　）​

  A． - 3 2

  B． - 3 3

  C． - 1 2

  D． - 3
  组卷：22引用：1难度：0.5

  解析

三．解答题

• 21．如图1，抛物线y=ax²+bx+3与x轴交于点A（-1，0）、点B，与y轴交于点C，顶点D的横坐标为1，对称轴交x轴于点E，交BC于点F．
  
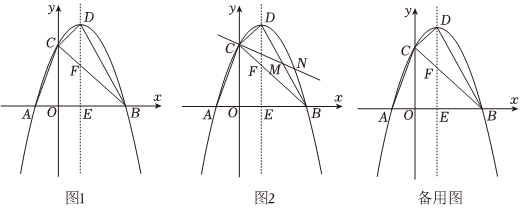
  （1）求顶点D的坐标；
  （2）如图2所示，过点C的直线交直线BD于点M，交抛物线于点N．
      ①若直线CM将△BCD分成的两部分面积之比为2：1，求点M的坐标；
      ②若∠NCB=∠DBC，求点N的坐标．
  组卷：44引用：1难度：0.3

  解析

• 22．如图
  
  （1）【问题发现】如图1，P是半径为2的⊙O上一点，直线m是⊙O外一直线，圆心O到直线m的距离为3，PQ⊥m于点Q，则PQ的最大值为_____；
  （2）【问题探究】如图2，将两个含有30°角的直角三角板的60°角的顶点重合（其中∠A=∠A′=30°，∠C=∠C'=90°），绕点B旋转△C′A′B，当旋转至CC′=4时，求AA′的长；
  （3）【问题解决】如图3，点O为等腰Rt△ABC的斜边AB的中点，AC=BC=5

  2

  ，OE=2，连接BE，作Rt△BEF，其中∠BEF=90°，tan∠EBF=

  3

  4

  ，连接AF，求四边形ACBF的面积的最大值．
  组卷：16引用：1难度：0.4

  解析