2023-2024学年浙江省金衢山五校联盟九年级（上）月考数学试卷（9月份）
发布：2024/8/20 12:0:1
一、选择题（本题有10小题，每小题3分，共30分.请选出各题中唯一的正确选项，不选、多选、错选，均不给分）
-
1．下列函数中，是二次函数的有（ ）
①y=3（x-1）2+1；②y=x+；③y=8x2+1；④y=3x3+2x2．1x组卷：298引用：4难度：0.7 -
2．对于二次函数y=3（x+4）2，其图象的顶点坐标为（ ）
组卷：86引用：10难度：0.6 -
3．将抛物线y=-
（x-2）2向右平移1个单位，再向下平移2个单位后，得到的抛物线解析式为（ ）13组卷：237引用：10难度：0.7 -
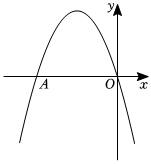4．如图，二次函数y=ax2+bx+c的图象与x轴交于A（-4，0）和原点，且顶点在第二象限．下列说法正确的是（ ）组卷：557引用：9难度：0.5 -
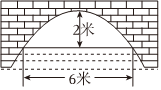5．如图是抛物线形拱桥，当拱顶离水面2米时，水面宽6米，则当水面宽8米时，水面下降了（ ）组卷：791引用：6难度：0.5 -
6．某种品牌的服装进价为每件150元，当售价为每件210元时，每天可卖出20件，现需降价处理，且经市场调查：每件服装每降价2元，每天可多卖出1件．在确保盈利的前提下，若设每件服装降价x元，每天售出服装的利润为y元，则y与x的函数关系式为（ ）
组卷：1988引用：9难度：0.9 -
7．已知抛物线y=-x2+2x+c,若点（0，y1）（1，y2）（3，y3）都在该抛物线上，则y1、y2、y3的大小关系是（ ）
组卷：1616引用：15难度：0.5 -
8．二次函数y=-x2+bx+c的图象的最高点是（-1，-3），则b,c的值分别是（ ）
组卷：1491引用：6难度：0.9
三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）
-
23．【阅读理解】：
关于x的函数y=mx-2m-3（m为常数，且m≠0），经过某个定点，请求出定点的坐标．
方法一：先将等式化为（x-2）m=y+3的形式，再根据0m=0时有m无数多个解，求得定点的坐标为（2，-3）；
方法二：当m=1时，y=x-5；当m=2时，y=2x-7；
解方程组解得y=x-5y=2x-7，x=2y=-3
∴求得定点的坐标为（2，-3）
【模仿练习】
关于x的二次函数 y=mx2+（2m+1）x+1（ 为常数，且m≠0），是否经过定点，如果是，请选择一种方法求出定点的坐标；如果不是，请说明理由．
【尝试应用】某“数学兴趣小组”根据学习函数的经验，对函数y=-（x-1）（|x|-3）的图象和性质进行了探究，探究过程如下，请补充完整：
（1）计算x与y的几组对应值，其中m=；
列表如下：x … -4 -3 -2 -1 0 1 2 3 4 … y … 5 0 -3 m -3 0 1 0 -3 … 
（2）如图，在直角坐标系中用描点法画出了函数y=-（x-1）（|x|-3）这个图象；
（3）若直线y=tx-2t+2与函数y=-（x-1）（|x|-3）（2＜x≤4）的图象只有一个交点，请结合函数图象，求出t的取值范围．组卷：254引用：3难度：0.3 -
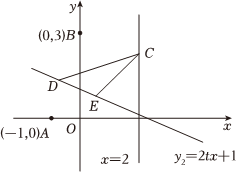24．“距离”是数学研究的重要对象，如我们所熟悉的两点间的距离．现在我们定义一种新的距离：已知P（a,b），Q（c,d）是平面直角坐标系内的两点，我们将|a-c|+|b-d|称作P，Q间的“L型距离”，记作L（P，Q），即L（P，Q）=|a-c|+|b-d|．
已知二次函数y1的图象经过平面直角坐标系内的A，B，C三点，其中A，B两点的坐标为A（-1，0），B（0，3），点C在直线x=2上运动，且满足L（B，C）≤BC．
（1）求L（A，B）；
（2）求抛物线y1的表达式；
（3）已知y2=2tx+1是该坐标系内的一个一次函数．
①若D，E是y2=2tx+1图象上的两个动点，且DE=5，求△CDE面积的最大值；
②当t≤x≤t+3时，若函数y=y1+y2的最大值与最小值之和为8，求实数t的值．组卷：537引用：4难度：0.1
