2022年湖北省武汉中学自主招生数学试卷

一、选择题：本题共6小题，每小题5分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知x²-5x-2022=0，则代数式

  （

  x

  -

  2

  ）

  4

  +

  （

  x

  -

  1

  ）

  2

  -

  1

  （

  x

  -

  1

  ）

  （

  x

  -

  2

  ）

  的值为（　　）

  A．2021

  B．2024

  C．2027

  D．2030
  组卷：349引用：2难度：0.7

  解析

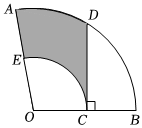• 2．如图，扇形OAB中，∠AOB=110°，OA=18，C是OB的中点，CD⊥OB交

  ˆ

  AB

  于点D，以OC为半径的

  ˆ

  CE

  交OA于点E，则图中阴影部分的面积是（　　）

  A． 12 π + 18 3

  B． 81 （ 3 + 2 π ） 2

  C． 81 （ 2 3 + π ） 4

  D． 6 π + 36 3
  组卷：176引用：4难度：0.5

  解析

• 3．2022年5月将迎来中国共产主义青年团成立100周年．武汉中学学工部将举行“青春有我，创武中明星班级”活动．学校安排高一3个班和高二2个班开展主题活动课，并随机从中抽两个班开放展示活动，则抽到高一、高二各1个班的概率是（　　）

  A． 1 2

  B． 1 5

  C． 2 3

  D． 3 5
  组卷：38引用：2难度：0.5

  解析

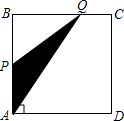• 4．如图，四边形ABCD是矩形，AB=8，BC=4，动点P以每秒2个单位的速度从点A沿线段AB向B点运动，同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动，当点Q到达点D时P、Q同时停止运动，若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是（　　）

  A．

  B．

  C．

  D．
  组卷：773引用：8难度：0.7

  解析

三、解答题：本题共4小题，共50分．解答应写出文字说明、证明过程或演算步骤．

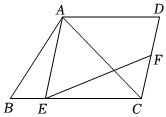• 13．四边形ABCD中，AD∥BC，∠BAC=∠D，点E在BC边上运动（不与C重合），点F在CD上运动，且∠AEF=∠ACD．
  （1）若AB=BC=CA，判断AE与EF的数量关系；
  （2）若AB=BC，你在（1）中得到的结论是否会发生变化？写出猜想并给出证明；
  （3）若AB=AC=5，

  sin

  ∠

  BAC

  =

  4

  5

  ，∠BAC为锐角，设EF=t,当E，F运动时，求t的取值范围．
  组卷：92引用：2难度：0.5

  解析

• 14．定义：由两条与x轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”．如图1，抛物线C₁与抛物线C₂组成一个开口向上的“月牙线”，抛物线C₁与抛物线C₂与x轴有相同的交点M，N（点M在点N的左侧），与y轴的交点分别为A，B且点A的坐标为（0，-3），抛物线C₂的解析式为y=mx²+4mx-12m（m＞0）．
  
  （1）求M，N两点的坐标；
  （2）在第三象限内的抛物线C₁上是否存在一点P，使得△PAM的面积最大？若存在，求出△PAM的面积的最大值；若不存在，说明理由；
  （3）如图2，若有一组成“月牙线”的抛物线C₃，C₄它们的解析式分别为C₃：

  y

  =

  -

  1

  8

  x

  2

  +

  1

  ，C₄：

  y

  =

  -

  1

  4

  x

  2

  ，P′为y轴上一点，过P′任意作一射线分别交C₃和C₄于N′，M′两点，过M′作直线y=1的垂线，垂足为G，过N′作直线y=3的垂线，垂足为H，是否存在这样的点P′，使P′M′=M′G，P′N′=N′H恒成立？若存在，求出点P′的坐标，并探究

  P

  ′

  M

  ′

  P

  ′

  N

  ′

  是否为定值，说明理由．
  组卷：290引用：3难度：0.1

  解析