当前位置：试卷中心 > 试卷详情

2023-2024学年湖南省湘潭市湘乡市名民实验学校高一（上）入学数学试卷

发布：2024/8/17 1:0:3

一、单选题（本题共8小题，每小题3分，共24分）

1．下列方程中，是关于x的一元二次方程的是（　　）
A．ax²+bx+c=0 B．x²-2x-1
C．
x
2
+
1
x
2
=
0
D．（x-1）（x+2）=1
组卷：32引用：1难度：0.9
解析
2．如图，在四个几何体中，三视图完全相同的几何体是（　　）
A．
正方体 B．
长方体 C．
圆锥 D．
圆柱
组卷：23引用：1难度：0.8
解析
3．下列计算，正确的是（　　）
A．a²•a³=a⁶ B．a²+a³=a⁵ C．（a³）²=a⁵ D．a²÷a³=a^-1
组卷：134引用：1难度：0.8
解析
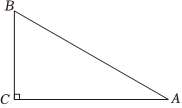4．如图，在Rt△ABC中，∠C=90°，AB=10，BC=6，sin∠B等于（　　）
A．
3
5
B．
3
4
C．
5
3
D．
4
5
组卷：40引用：1难度：0.8
解析
5．若两个相似三角形的周长之比为3：5，则这两个三角形的面积之比为（　　）
A．3：5 B．3：8 C．9：15 D．9：25
组卷：7引用：1难度：0.9
解析
6．二次函数y=-（x-1）²+3的图象的顶点坐标是（　　）
A．（-1，3） B．（1，3） C．（-1，-3） D．（1，-3）
组卷：95引用：1难度：0.9
解析
7．若x²-2（m+4）x+25是一个完全平方式，则m的值为（　　）
A．1或-9 B．2 C．3 D．5或1
组卷：47引用：1难度：0.8
解析
8．若数轴上表示数x的点在原点的左边，则化简
|
3
x
+
x
2
|
的结果是（　　）
A．-4x B．4x C．-2x D．2x
组卷：29引用：1难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（72分）

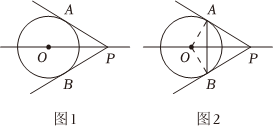25．请阅读材料，并完成相应的任务：学习了圆的切线以后，某课外小组的同学们发现，过圆外一点可以画圆的两条切线．如图1，P为⊙O外一点，过点P可以画⊙O的两条切线PA，PB．切点分别为A，B．
[发现结论]智慧小组在操作中发现，沿直线OP将图形对折，可以得出结论：PA=PB，∠APO=∠BPO．
[证明结论]启迪小组为了证明上述结论的正确性，做了如下证明：
如图2，连接OA和OB．
∵PA，PB是⊙O的两条切线，
∴PA⊥OA，PB⊥OB．（依据）
∴∠PAO=∠PBO=90°．
…
任务：
（1）请写出括号中的依据：_____；
（2）请将上面的证明过程补充完整；
（3）如图2，在⊙O中，PA，PB为⊙O的两条切线，A，B分别为它们的切点，⊙O的半径为5，∠APB=60°．连接AB，请直接写出△PAB的周长．
组卷：5引用：1难度：0.5
解析
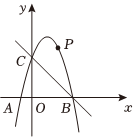26．如图，在平面直角坐标系中，二次函数y=-x²+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0），点P是抛物线上一个动点，且在直线BC的上方．
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，使△BPC的面积最大，求出点P的坐标和△BPC的面积最大值．
组卷：35引用：1难度：0.7
解析