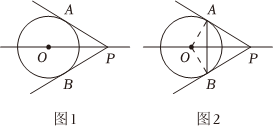
请阅读材料，并完成相应的任务：学习了圆的切线以后，某课外小组的同学们发现，过圆外一点可以画圆的两条切线．如图1，P为⊙O外一点，过点P可以画⊙O的两条切线PA，PB．切点分别为A，B．
[发现结论]智慧小组在操作中发现，沿直线OP将图形对折，可以得出结论：PA=PB，∠APO=∠BPO．
[证明结论]启迪小组为了证明上述结论的正确性，做了如下证明：
如图2，连接OA和OB．
∵PA，PB是⊙O的两条切线，
∴PA⊥OA，PB⊥OB．（依据）
∴∠PAO=∠PBO=90°．
…
任务：
（1）请写出括号中的依据：_____；
（2）请将上面的证明过程补充完整；
（3）如图2，在⊙O中，PA，PB为⊙O的两条切线，A，B分别为它们的切点，⊙O的半径为5，∠APB=60°．连接AB，请直接写出△PAB的周长．