2023-2024学年河南省洛阳第一高级中学高二（上）期中数学试卷（B卷）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦点分别为F₁，F₂，P为椭圆C上一点，若△PF₁F₂的周长为18，长半轴长为5，则椭圆C的离心率为（　　）

  A． 3 4

  B． 4 5

  C． 2 3

  D． 2 2 5
  组卷：438引用：6难度：0.7

  解析

• 2．如图，圆台的高为4，上、下底面半径分别为3，5，O₁，O₂分别为下底面圆和上底面圆的圆心，M，N分别在上、下底面圆的圆周上，且

  〈

  O

  2

  M

  ，

  O

  1

  N

  〉

  =

  120

  °

  ，则

  |

  MN

  |

  =（　　）

  A． 65

  B． 5 2

  C． 35

  D．5
  组卷：24引用：1难度：0.5

  解析

• 3．若动点A，B分别在直线l₁：x+y-7=0和l₂：x+y-5=0上移动，则AB的中点M到原点的距离的最小值为（　　）

  A．3 2

  B．2 2

  C．3 3

  D．4 2
  组卷：1582引用：11难度：0.7

  解析

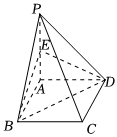• 4．如图，四棱锥P-ABCD的底面ABCD是菱形，AB=4，∠ABC=60°，PA⊥平面ABCD，且PA=4，E是PA的中点，则PC到平面BED的距离为（　　）

  A． 2

  B． 3

  C． 2 2

  D． 2 3
  组卷：58引用：4难度：0.5

  解析

• 5．若圆C：x²+y²+2x-4y+3=0关于直线2ax+by+6=0对称，则由点（a,b）向圆C所作切线长的最小值是（　　）

  A．2

  B．3

  C．4

  D．6
  组卷：1701引用：67难度：0.7

  解析

• 6．已知抛物线C：y²=2px（p＞0）的焦点为F，经过点

  P

  （

  -

  p

  2

  ，

  0

  ）

  且斜率为

  2

  2

  3

  的直线l与抛物线C交于A，B两点，若|AF|=2|BF|，且

  S

  △

  BOF

  =

  2

  2

  ，则p=（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：188引用：2难度：0.5

  解析

四、解答题：本题共4题，每小题10分，共40分.解答应写出文字说明、证明过程或演算步骤.

• 19．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦点分别为F₁，F₂，斜率为-3的直线l与双曲线C交于A，B两点，点

  M

  （

  4

  ，-

  2

  2

  ）

  在双曲线C上，且|MF₁|•|MF₂|=24．
  （1）求△MF₁F₂的面积；
  （2）若

  OB

  +

  OB

  ′

  =

  0

  （O为坐标原点），点N（3，1），记直线NA，NB'的斜率分别为k₁，k₂，问：k₁•k₂是否为定值？若是，求出该定值；若不是，请说明理由．
  组卷：365引用：4难度：0.4

  解析

• 20．已知抛物线C：y²=2px（p＞0），抛物线C上横坐标为1的点到焦点F的距离为3．
  （Ⅰ）求抛物线C的方程及其准线方程；
  （Ⅱ）过（-1，0）的直线l交抛物线C于不同的两点A，B，交直线x=-4于点E，直线BF交直线x=-1于点D．是否存在这样的直线l,使得DE∥AF？若不存在，请说明理由；若存在，求出直线l的方程．
  组卷：501引用：5难度：0.6

  解析