2023年上海交大附中高考数学练习试卷（8）

一、填空题（本大题共有12题，满分36分，请在空格内直接填写结果，1-6题每个空格填对得4分，7-12题每个空格填对得5分，否则一律得0分）

• 1．已知集合A={y|y=2^x}，B={x|y=lg（x-1）}，则A∩

  B

  =

  ．
  组卷：77引用：1难度：0.7

  解析

• 2．已知

  sinα

  =

  1

  3

  ，则

  tanα

  -

  cosα

  tanα

  +

  cosα

  的值为

  ．
  组卷：148引用：1难度：0.7

  解析

• 3．已知

  a

  =（1，3），

  b

  =（4，-3），则

  a

  在

  b

  方向上的投影为

  ．
  组卷：85引用：1难度：0.9

  解析

• 4．已知z=（a+i）（2-i）（其中a∈R，i为虚数单位），若复数z在复平面内对应的点位于第一象限，则a的取值范围是

  ．
  组卷：97引用：1难度：0.7

  解析

• 5．已知一个圆锥的侧面展开图是一个半径为4厘米，圆心角为90°的扇形，则该圆锥的体积是

  立方厘米．
  组卷：67引用：1难度：0.6

  解析

• 6．若不等式ax²+bx+2＞0的解集为（-1，2），则不等式2x²+bx+a＞0的解集为

  ．
  组卷：426引用：1难度：0.7

  解析

• 7．若圆C：（x-2）²+（y-m）²=4上总存在点到直线l：x+y-2=0的距离等于1，则实数m的取值范围是

  ．
  组卷：104引用：1难度：0.6

  解析

三、解答题（本题共5题，共78分，解答本大题需写出必要的过程）

• 20．已知n∈Z且n＞0，f_n（x）=sinnx+nsinx.
  （1）若f_n（

  π

  2

  ）=2022，求n的值；
  （2）求函数y=f₂（x）的单调增区间；
  （3）猜测函数y=f_n（x）的最小正周期，并证明之．
  组卷：66引用：1难度：0.5

  解析

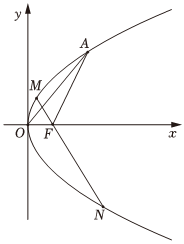• 21．已知抛物线C：y²=4x,点F是其焦点，点A是抛物线C在第一象限内的一个动点．在△OAF中，作∠OFA的平分线所在直线交抛物线C于M、N两点．
  （1）若

  MF

  =

  1

  4

  FN

  ，求|MN|．
  （2）设直线的斜率为k₁，直线MN的斜率为k₂，证明：k₁•k₂是定值，并求出该定值．
  （3）过F作直线OA的平行线交抛物线C于P、Q两点．求四边形PMQN面积的最小值，并求出此时点A的坐标．
  组卷：76引用：1难度：0.5

  解析