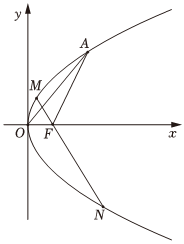
已知抛物线C：y2=4x,点F是其焦点，点A是抛物线C在第一象限内的一个动点．在△OAF中，作∠OFA的平分线所在直线交抛物线C于M、N两点．
（1）若MF=14FN，求|MN|．
（2）设直线的斜率为k1，直线MN的斜率为k2，证明：k1•k2是定值，并求出该定值．
（3）过F作直线OA的平行线交抛物线C于P、Q两点．求四边形PMQN面积的最小值，并求出此时点A的坐标．
MF
=
1
4
FN
【答案】（1）；（2）-2；（3）12．
25
4
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/18 8:0:8组卷：76引用：1难度：0.5
相似题
-
1．抛物线x2=4y的焦点为F，准线为l,A，B是抛物线上的两个动点，且满足AF⊥BF，P为线段AB的中点，设P在l上的射影为Q，则
的最大值是（ ）|PQ||AB|发布：2024/12/29 5:30:3组卷：479引用：8难度：0.5 -
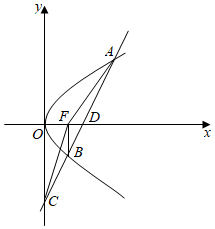2．如图，设抛物线y2=2px的焦点为F，过x轴上一定点D（2，0）作斜率为2的直线l与抛物线相交于A，B两点，与y轴交于点C，记△BCF的面积为S1，△ACF的面积为S2，若，则抛物线的标准方程为（ ）S1S2=14发布：2024/12/17 0:0:2组卷：164引用：6难度：0.6 -
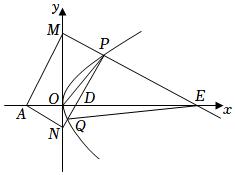3．如图，已知点P是抛物线C：y2=4x上位于第一象限的点，点A（-2，0），点M，N是y轴上的两个动点（点M位于x轴上方），满足PM⊥PN，AM⊥AN，线段PN分别交x轴正半轴、抛物线C于点D，Q，射线MP交x轴正半轴于点E．
（Ⅰ）若四边形ANPM为矩形，求点P的坐标；
（Ⅱ）记△DOP，△DEQ的面积分别为S1，S2，求S1•S2的最大值．发布：2024/12/29 1:0:8组卷：98引用：2难度：0.4
