2022-2023学年浙江省宁波市镇海区立人中学九年级（上）期中数学试卷

一．选择题（共10小题，每题4分，共40分）

• 1．一个不透明的袋子里装有3个黑球和4个白球，每个球除颜色外其他都相同，从中随机摸出1个球，摸到白球的概率是（　　）

  A． 1 7

  B． 3 7

  C． 4 7

  D． 1 4
  组卷：94引用：2难度：0.9

  解析

• 2．同圆中，已知

  ˆ

  AB

  所对的圆心角是80°，则

  ˆ

  AB

  所对的圆周角度数（　　）

  A．40°

  B．80°

  C．100°

  D．120°
  组卷：350引用：2难度：0.8

  解析

• 3．两个相似多边形的周长之比为1：4，则它们的面积之比为（　　）

  A．1：2

  B．1：4

  C．1：8

  D．1：16
  组卷：1536引用：12难度：0.8

  解析

• 4．将二次函数

  y

  =

  1

  3

  x

  2

  的图象向右平移1个单位，所得图象的解析式为（　　）

  A． y = 1 3 （ x - 1 ） 2

  B． y = 1 3 （ x + 1 ） 2

  C． y = 1 3 x 2 + 1

  D． y = 1 3 x 2 - 1
  组卷：219引用：3难度：0.8

  解析

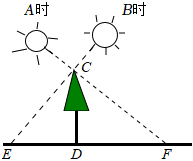• 5．如图，嘉嘉在A时测得一棵4米高的树的影长DF为8m,若A时和B时两次日照的光线互相垂直，则B时的影长DE为（　　）

  A．2m

  B．2 5 m

  C．4m

  D．4 2 m
  组卷：1113引用：9难度：0.5

  解析

• 6．如图，AB为⊙O的直径，弦CD交AB于点E，BC=BD，∠CDB=30°，AC=2

  3

  ，则OE=（　　）

  A． 3 2

  B． 3

  C．2

  D．1
  组卷：903引用：16难度：0.7

  解析

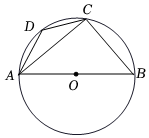• 7．如图，AB为⊙O的直径，点C，D在⊙O上，若∠ADC=130°，则∠BAC的度数为（　　）

  A．25°

  B．30°

  C．40°

  D．50°
  组卷：2416引用：21难度：0.7

  解析

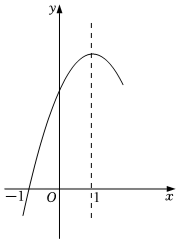• 8．如图，抛物线y=ax²+bx+c（a≠0）与x轴的一个交点坐标为（-1，0），抛物线的对称轴为直线x=1，下列结论：①abc＜0；②3a+c=0；③当y＞0时，x的取值范围是-1≤x＜3；④点（-2，y₁），（2，y₂）都在抛物线上，则有y₁＜0＜y₂.其中结论正确的个数是（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：2525引用：16难度：0.5

  解析

三．解答题（共8小题）

• 23．阅读理解：
  从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
  （1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
  （2）在△ABC中，∠A=48°，CD为△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．
  组卷：1130引用：5难度：0.3

  解析

• 24．如图，AB为⊙O直径，点D为AB下方⊙O上一点，点C为弧ABD中点，连接CD，CA．
  （1）求证：∠ABD=2∠BDC；
  （2）过点C作CE⊥AB于H，交AD于E，求证：EA=EC；
  （3）在（2）的条件下，若OH=5，AD=24，求线段DE的长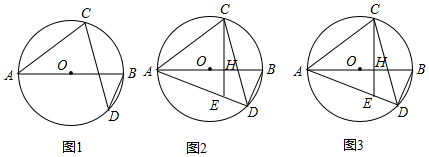
  
  组卷：6965引用：10难度：0.3

  解析