2023-2024学年河南省名校创新发展联盟高二（上）第一次联考数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．在空间直角坐标系Oxyz中，点A（2，3，6）在坐标平面Oxz内的射影为点B，则B的坐标为（　　）

  A．（0，3，6）

  B．（2，0，6）

  C．（2，3，0）

  D．（2，0，3）
  组卷：48引用：10难度：0.8

  解析

• 2．某工厂生产甲、乙、丙三种不同型号的产品，产量分别为200件、300件、400件．为检验产品的质量，现用分层抽样的方法，从以上所有的产品中抽取了45件进行检验，则抽取的甲、乙种型号产品的数量之和为（　　）

  A．30

  B．15

  C．20

  D．25
  组卷：39引用：3难度：0.8

  解析

• 3．若

  z

  =

  3

  -

  i

  1

  +

  i

  ，则z+

  z

  =（　　）

  A．-2

  B．-2i

  C．2

  D．2i
  组卷：23引用：3难度：0.8

  解析

• 4．抛掷一枚质地均匀的骰子1次，事件A表示“掷出的点数大于2”，则与A互斥且不对立的事件是（　　）

  A．掷出的点数为偶数	B．掷出的点数为奇数
  C．掷出的点数小于2	D．掷出的点数小于3
  组卷：80引用：5难度：0.7

  解析

• 5．已知圆锥的底面半径为4，其侧面展开图是一个圆心角为

  8

  π

  5

  的扇形，则该圆锥的体积为（　　）

  A．48π

  B．45π

  C．16π

  D．15π
  组卷：445引用：7难度：0.8

  解析

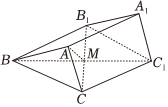• 6．如图，在三棱柱ABC-A₁B₁C₁中，AB=AC=2，AA₁=3，∠BAC=60°，∠A₁AC=∠A₁AB=120°，B₁C与BC₁的交点为M，则AM=（　　）

  A． 1 2

  B． 5 4

  C． 3 2

  D． 10 4
  组卷：55引用：6难度：0.7

  解析

• 7．在正三棱柱ABC-A₁B₁C₁中，

  AB

  =

  3

  ，点D在棱BC上运动，若AD+DB₁的最小值为

  13

  ，则三棱柱ABC-A₁B₁C₁的外接球的表面积为（　　）

  A．8π

  B．16π

  C．20π

  D．32π
  组卷：154引用：10难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤．

• 21．A，B，C，D四人参加双淘汰赛制比赛．在第一轮的两场比赛中，A对B，C对D，这两场比赛的胜者进入优胜组，负者进入奋斗组．第二轮的两场比赛分别为优胜组和奋斗组的组内比赛，奋斗组中的胜者与优胜组中的负者均进入超越组，奋斗组中的负者直接被淘汰，优胜组中的胜者进入卓越组，第三轮比赛为超越组组内比赛，胜者进入卓越组，负者为季军．第四轮比赛为卓越组组内比赛，胜者为冠军，负者为亚军，每轮比赛都相互独立．
  （1）设A，B，C，D四人每轮比赛的获胜率均为

  1

  2

  ．
  ①求A和B都进入卓越组的概率；
  ②求D参加了四轮比赛并获得冠军的概率．
  （2）若B每轮比赛的获胜率为

  2

  3

  ，A，C，D三人水平相当，求A，C进入卓越组且A，C之前赛过一场的概率．
  组卷：63引用：3难度：0.6

  解析

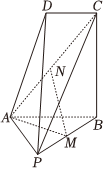• 22．如图，在四棱锥P-ABCD中，平面ABCD⊥平面PAB，

  ∠

  ABC

  =∠

  PAB

  =∠

  BCD

  =

  π

  2

  ，PA=AB=BC=2CD=2，点M，N分别在线段PB，AC上．
  （1）当M，N分别是PB，AC的中点时，证明：AB⊥MN．
  （2）当MN的长度最小时，求直线PB与平面AMN所成角的大小．
  组卷：73引用：3难度：0.5

  解析