当前位置：试卷中心 > 试卷详情

2022-2023学年湖北省鄂东南教学改革联盟学校高一（下）期中数学试卷

发布：2024/7/20 8:0:8

一、选择题（本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1．已知集合A={0，a}，B={2^a，b}，若A∪B={0，1，2}，则b=（　　）
A．0 B．1 C．0或1 D．2
组卷：78引用：2难度：0.8
解析
2．若复数
z
=
a
-
i
1
+
i
（
a
∈
R
）
是纯虚数，则z的共轭复数
z
=（　　）
A．-1 B．-i C．i D．1
组卷：27引用：4难度：0.8
解析
3．“
φ
=
-
π
2
”是“函数y=sin（x+φ）为偶函数”的（　　）条件．
A．充分不必要 B．必要不充分
C．充要 D．既不充分也不必要
组卷：29引用：4难度：0.7
解析
4．下列各式中，其值为
1
2
的是（　　）
A．
co
s
2
π
12
-
si
n
2
π
12
B．
1
2
tan
22
.
5
°
1
-
tan
2
22
.
5
°
C．sin15°cos15°
D．
1
+
cos
2
π
3
2
组卷：74引用：2难度：0.7
解析
5．牛奶的保鲜时间因储藏温度的不同而不同，假定保鲜时长t（单位：h）与储藏温度x（单位：℃）之间的关系为
t
=
192
×
（
7
32
）
x
22
，若要使牛奶保鲜时长超过96h,则应储藏在温度低于（　　）℃的环境中．（附：lg2≈0.301，lg7≈0.845，答案采取四舍五入精确到0.1）
A．10.0 B．10.3 C．10.5 D．10.7
组卷：51引用：3难度：0.6
解析
6．已知向量
a
=（1，2），
b
=（-4，t），则下列说法错误的是（　　）
A．若
a
∥
b
，则t=-8
B．|
a
-
b
|_min=5
C．若
|
a
+
b
|
=
|
a
-
b
|
，则t=2
D．若
a
与
b
的夹角为钝角，则t＜2
组卷：106引用：2难度：0.5
解析
7．将函数
y
=
2
cos
（
x
-
π
3
）
的图象向右平移m（0＜m＜π）个单位长度后得到f（x）的图象．若f（x）在
（
π
6
，
5
π
6
）
上单调递增，则m的取值范围为（　　）
A．
[
π
3
，
π
2
]
B．
[
π
6
，
π
2
]
C．
[
π
3
，
2
π
3
]
D．
[
π
2
，
5
π
6
]
组卷：71引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

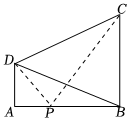21．如图，为了测量某条河流两岸两座高塔底部A，B之间的距离，观测者在其中一座高塔的顶部D测得另一座高塔底部B和顶部C的视角为45°（即∠BDC=45°），已知两座高塔的高AD为30m,BC为75m,塔底A，B在同一水平面上，且AD⊥AB，BC⊥AB．
（1）求两座高塔底部A，B之间的距离；
（2）为庆祝2023年春节的到来，在两座高塔顶部各安装了一个大型彩色灯饰．政府部门为了方便市民观赏这两个彩色灯饰，决定在A，B之间的点P处（点P在线段AB上）搭建一个水上观景台，为了达到最佳的观赏效果，要求∠DPC最大，问：在距离A点多远处搭建，才能达到最佳的观赏效果？
组卷：47引用：4难度：0.4
解析
22．已知函数
f
（
x
）
=
lnx
-
x
+
1
x
-
1
．
（1）求值：
f
（
2
）
+
f
（
1
2
）
+
f
（
3
）
+
f
（
1
3
）
+
⋯
+
f
（
2023
）
+
f
（
1
2023
）
；
（2）判断函数f（x）的单调性，并证明你的结论：
（3）求证f（x）有且仅有两个零点x₁、x₂并求x₁x₂的值．
组卷：45引用：4难度：0.4
解析