当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省金华市东阳中学、东阳外国语学校高一（下）期中数学试卷

发布：2024/5/25 8:0:9

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个

1．已知复数z满足（1+i）z=2i（i为虚数单位），则|
z
|=（　　）
A．
2
B．1 C．2 D．4
组卷：27引用：1难度：0.9
解析
2．已知向量
a
=
（
2
，
1
）
，
a
•
b
=
10
，
|
a
+
b
|
=
5
2
，则
|
b
|
=（　　）
A．
5
B．
10
C．5 D．25
组卷：98引用：7难度：0.6
解析
3．棱长为4的正方体的内切球的表面积为（　　）
A．4π B．12π C．16π D．20π
组卷：297引用：7难度：0.9
解析
4．冬奥会会徽以汉字“冬”为灵感来源，结合中国书法的艺术形态，将悠久的中国传统文化底蕴与国际化风格融为一体，呈现出中国在新时代的新形象、新梦想．某同学查阅资料得知，书法中的一些特殊画笔都有固定的角度，比如弯折位置通常采用30°、45°、60°、90°、120°、150°等特殊角度下．为了判断“冬”的弯折角度是否符合书法中的美学要求．该同学取端点绘制了△ABD，测得AB=5，BD=6，
AC
=
14
，AD=3，若点C恰好在边BD上，请帮忙计算sin∠ACD的值（　　）
A．
1
2
B．
5
9
C．
2
3
D．
2
14
9
组卷：87引用：4难度：0.6
解析
5．设α、β是互不重合的平面，1、m、n是互不重合的直线，下列命题正确的是（　　）
A．若m⊂α，n⊂α，l⊥m,l⊥n,则l⊥α
B．若l⊥n,m⊥n,则l∥m
C．若m∥α，n∥β，α⊥β，则m⊥n
D．若l⊥α，l∥β，则α⊥β
组卷：253引用：12难度：0.6
解析
6．已知命题
p
：
2
x
x
-
1
＜
1
，命题q：（x-a）（x-3）＞0，若p是q的充分不必要条件，则实数a的取值范围是（　　）
A．（-∞，1] B．[1，3] C．[1，+∞） D．[3，+∞）
组卷：77引用：4难度：0.8
解析
7．已知a=2sin1，b=
3
6
，
c
=
2
0
.
99
，则a,b,c的大小关系是（　　）
A．c＜b＜a B．a＜c＜b C．c＜a＜b D．a＜b＜c
组卷：51引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

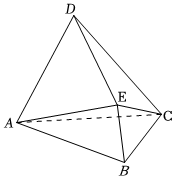21．如图，在多面体ABCDE中，平面ACD⊥平面ABC，BE⊥平面ABC，△ABC和△ACD均为正三角形，AC=4，BE=
3
．
（1）在线段AC上是否存在点F，使得BF∥平面ADE？若存在，确定F的位置；若不存在，说明理由；
（2）求平面CDE与平面ADC所成的锐二面角的正切值．
组卷：53引用：1难度：0.5
解析
22．已知函数g（x）=x²-2ax+1，且函数y=g（x+1）是偶函数，设f（x）=
g
（
x
）
x
．
（1）求f（x）的解析式；
（2）若不等式f（lnx）-mlnx≥0在区间（1，e²]上恒成立，求实数m的取值范围；
（3）若方程f（|2^x-1|）+k•
2
|
2
x
-
1
|
-2=0有三个不同的实数根，求实数k的取值范围．
组卷：246引用：6难度：0.3
解析