当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省绍兴市柯桥区联盟校九年级（上）课堂作业数学试卷（二）（12月份）

发布：2024/7/24 8:0:9

一、选择题（每题4分，共40分）

1．已知
a
b
=
2
3
，则
a
+
b
a
的值为（　　）
A．
5
2
B．
5
3
C．
3
2
D．
2
3
组卷：148引用：10难度：0.9
解析
2．抛物线y=x²-2x+3的顶点坐标是（　　）
A．（1，3） B．（-1，3） C．（1，2） D．（-1，2）
组卷：1003引用：13难度：0.9
解析
3．下列事件中，属于必然事件的是（　　）
A．小明买彩票中奖
B．在一个只有红球的盒子里摸球，摸到了白球
C．任意抛掷一只纸杯，杯口朝下
D．任选三角形的两边，其差小于第三边
组卷：124引用：2难度：0.8
解析
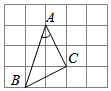4．在4×5网格中，A，B，C为如图所示的格点（正方形的顶点），则下列等式正确的是（　　）
A．sinA=
3
2
B．cosA=
1
2
C．tanA=
3
3
D．cosA=
2
2
组卷：600引用：3难度：0.6
解析
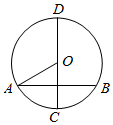5．如图，已知⊙O的半径为3，弦AB⊥直径CD，∠A=30°，则
ˆ
BD
的长为（　　）
A．π B．2π C．3π D．6π
组卷：623引用：6难度：0.5
解析
6．把二次函数y=（x-1）²-3的图象向左平移3个单位，向上平移4个单位后，得到的图象所对应的二次函数表达式为（　　）
A．y=（x+2）²+1 B．y=（x-2）²+1
C．y=（x+4）²+1 D．y=（x-4）²+1
组卷：503引用：6难度：0.8
解析
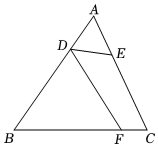7．如图，在△ABC中，AB≠AC，AC=3AD，AB=3AE，点F为边BC上一点，则下列条件不能保证△FDB与△ADE相似的是（　　）
A．∠A=∠BFD B．DF∥AC C．
BD
DE
=
DF
AD
D．
BD
AE
=
BF
DE
组卷：12引用：1难度：0.5
解析
8．如图1是一个小区入口的双翼闸机，它的双翼展开时，双翼边缘的端点A与B之间的距离为8cm（如图2），双翼的边缘AC=BD=60cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°．当双翼收起时，可以通过闸机的物体的最大宽度为（　　）
A．60
3
+8 B．60
2
+8 C．64 D．68
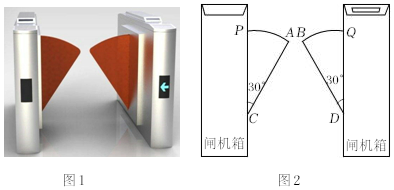组卷：989引用：16难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

23．我们把一直角边是另一直角边2倍的直角三角形称为“倍勾三角形”，如图1，在△ABC中，AB=3，AC=2
2
，∠BAC=45°，CD⊥AB于D．P是射线AB上的一个动点（不与D重合），E是线段PC的中点，将点E绕点P顺时针方向旋转90°得到点F，连接FB，FC，FP．
（1）下列三角形：①△PCF，②△BCD，③△ACD，其中是“倍勾三角形”的有
（填序号）；
（2）求证：CB⊥BF；
（3）连接FA，如图2，当F，E，A三点在一直线上时，△BCF是否为“倍勾三角形”，如果是，请证明；如果不是，求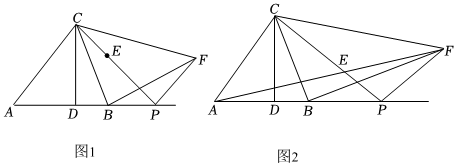
BF
BC
的值．
组卷：16引用：1难度：0.5
解析
24．如图，在矩形ABCD中，AB=8，BC=4，点E是AD上一点，且AE=1，F是边AB上的动点，以EF为边作矩形EFGH，使EH=
1
2
EF，矩形E'F'G'H'是矩形EFGH关于对角线BD的轴对称图形．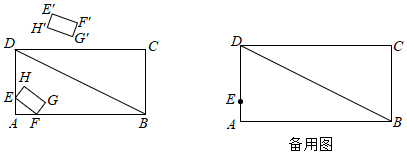

（1）当EF∥BD时，求矩形EFGH的面积．
（2）当点G'落在BD上时，求tan∠GFB．
（3）在F从A到B的运动过程中，
①当G'落在边CD上时，求AF的长．
②当矩形E'F'G'H'与矩形ABCD的边只有两个交点时，直接写出AF的取值范围．
组卷：117引用：4难度：0.3
解析