2023-2024学年湖南省岳阳十三中高一（上）入学数学试卷

一、单选题：（本题共12小题，每小题5分，共60分）

• 1．下列运算正确的是（　　）

  A． （ 2 3 - 5 ） （ 2 3 + 5 ） = 1	B． 125 - 45 = 2 5
  C． 28 ÷ （ - 1 2 7 ） = - 8	D． si n 2 60 ° + 2 3 = 5 3 2
  组卷：41引用：1难度：0.8

  解析

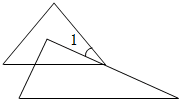• 2．将一副三角板如图所示放置，斜边平行，则∠1的度数为（　　）

  A．5°

  B．10°

  C．15°

  D．20°
  组卷：25引用：2难度：0.9

  解析

• 3．已知

  a

  -

  1

  a

  =

  7

  ，则

  a

  +

  1

  a

  =（　　）

  A． ± 3

  B．±3

  C． ± 11

  D．±11
  组卷：265引用：2难度：0.8

  解析

• 4．世界近代三大数学难题之一哥德巴赫猜想于1742年由哥德巴赫在给欧拉的信中提出：任一大于2的偶数都可写成两个奇素数之和．这个猜想至今没有完全证明，目前最前沿的成果是1966年我国数学家陈景润证明了“1+2”，即他证明了任何一个充分大的偶数，都可以表示为两个数之和，其中一个是素数，另一个或为素数，或为两个素数的乘积，被称为“陈氏定理”．我们知道素数又叫质数，是指在大于1的自然数中，除了1和它本身以外，不能被其他自然数整除的数．请问同学们，如果我们从不大于8的自然数中任取两个不同的数，这个两个数都是素数有多少种不同的情况？（　　）

  A．6

  B．10

  C．12

  D．16
  组卷：45引用：2难度：0.8

  解析

• 5．下列选项中的垃圾分类图标，既是中心对称图形，又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1引用：1难度：0.7

  解析

• 6．△ABC中，若∠A：∠B：∠C=1：2：3，G为△ABC的重心，则△GAB面积：△GBC面积：△GAC面积=（　　）

  A．1：2： 3

  B．1： 3 ：2

  C．2：1： 3

  D．1：1：1
  组卷：10引用：1难度：0.7

  解析

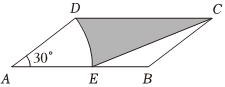• 7．如图，在平行四边形ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（　　）

  A． 2 - π 3

  B． 3 - π 3

  C． 3 3 - π 3

  D． 2 3 - π 3
  组卷：49引用：1难度：0.8

  解析

三、解答题：（本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

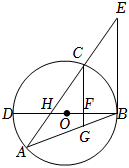• 21．如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A=∠EBC．
  （1）求证：BE是⊙O的切线；
  （2）已知CG∥EB，且CG与BD，BA分别相交于点F，G，若BG•BA=48，FG=

  2

  ，DF=2BF，求AH的值．
  组卷：71引用：3难度：0.3

  解析

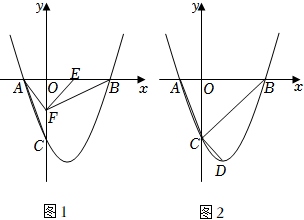• 22．在平面直角坐标系中，抛物线y=x²-2x-3与x轴相交于点A，B（点A在点B的左侧），与y轴相交于点C，连接AC．
  （1）求点B，点C的坐标；
  （2）如图1，点E（m,0）在线段OB上（点E不与点B重合），点F在y轴负半轴上，OE=OF，连接AF，BF，EF，设△ACF的面积为S₁，△BEF的面积为S₂，S=S₁+S₂，当S取最大值时，求m的值；
  （3）如图2，抛物线的顶点为D，连接CD，BC，点P在第一象限的抛物线上，PD与BC相交于点Q，是否存在点P，使∠PQC=∠ACD，若存在，请求出点P的坐标；若不存在，请说明理由．
  组卷：104引用：2难度：0.4

  解析