2022-2023学年浙江省S9联盟高一（下）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合U={-2，-1，0，1，2，3}，A={-1，0，1}，B={1，2，3}，则∁_U（A∩B）=（　　）

  A．{-2，3}	B．{-2，2，3}
  C．{-2，-1，0，3}	D．{-2，-1，0，2，3}
  组卷：101引用：2难度：0.9

  解析

• 2．设i为虚数单位，复数z满足（1+i）z=-1+i,则z•

  z

  为（　　）

  A． 2

  B．1

  C．3

  D． 3 2
  组卷：116引用：5难度：0.8

  解析

• 3．在△ABC中，已知p：A=B，q：sinA=sinB，则p是q的（　　）条件

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分也不必要
  组卷：82引用：4难度：0.7

  解析

• 4．已知，

  a

  =

  lo

  g

  3

  3

  ，

  b

  =

  lo

  g

  4

  3

  ，c=0.3^-1，则（　　）

  A．a＞b＞c

  B．b＞c＞a

  C．c＞a＞b

  D．c＞b＞a
  组卷：152引用：3难度：0.7

  解析

• 5．在△ABC中，D为BC的中点，E为AC边上的点，且

  AE

  =

  1

  3

  EC

  ，则

  ED

  =（　　）

  A． 1 2 AB + 1 4 AC

  B． 1 2 AB - 2 3 AC

  C． - 1 2 AB + 1 4 AC

  D． - 1 2 AB + 2 3 AC
  组卷：185引用：4难度：0.7

  解析

• 6．在△ABC中，已知b²+c²-a²=bc,且2cosBsinC=sinA，则该三角形的形状是（　　）

  A．直角三角形

  B．等腰三角形

  C．等边三角形

  D．钝角三角形
  组卷：161引用：4难度：0.8

  解析

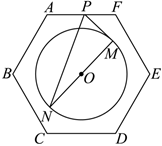• 7．已知图中正六边形ABCDEF的边长为6，圆O的圆心为正六边形的中心，直径为4，若点P在正六边形的边上运动，MN为圆O的直径，则

  PM

  •

  PN

  的取值范围是（　　）

  A．[26，35]

  B．[24，33]

  C．[25，35]

  D．[23，32]
  组卷：104引用：2难度：0.6

  解析

四、解答题：本题共6小题.共70分，解答应写出文字说明，证明过程或演算步骤.

• 21．在平面直角坐标系中，已知

  A

  （

  n

  ,

  2

  n

  ）

  ，

  B

  （

  8

  -

  m

  ,

  8

  -

  3

  2

  m

  ）

  ，

  C

  （

  7

  -

  m

  ,

  0

  ）

  ，

  n

  ,

  m

  ∈

  R

  ，

  n

  ≠

  0

  ．
  （1）若m=4，P为x轴上的一动点，点A′（2，-4），当A′，P，B三点共线时，求点P的坐标；
  （2）若n=sinθ，θ∈（0，π），且

  CA

  与

  CB

  的夹角

  α

  ∈

  [

  0

  ，

  π

  2

  ）

  ，求m的取值范围．
  组卷：52引用：2难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  x

  +

  4

  x

  -

  5

  （

  x

  ＞

  0

  ）

  ．
  （1）证明：函数f（x）在（0，2）上单调递减；
  （2）讨论关于x的方程|f（x）|=k（k∈R）的实数解的个数．
  组卷：72引用：3难度：0.5

  解析