当前位置：试卷中心 > 试卷详情

2023-2024学年广东省广州市真光中学高二（上）期中数学试卷

发布：2024/10/2 4:0:2

一、单选题（本题共8小题，每小题5分，共40分）

1．已知A（1，1，1），B（3，3，3），O为坐标原点，求
OA
与
BO
的夹角（　　）
A．0 B．
π
2
C．π D．
3
π
4
组卷：36引用：3难度：0.9
解析
2．过点A（-6，2），B（2，-2）且圆心在直线x-y+1=0上的圆的方程是（　　）
A．（x-3）²+（y-2）²=25 B．（x+3）²+（y+2）²=5
C．（x-3）²+（y-2）²=5 D．（x+3）²+（y+2）²=25
组卷：886引用：7难度：0.8
解析
3．已知直线：l₁：y=ax+3与l₂关于直线y=x对称，l₂与l₃：x+2y-1=0平行，则a=（　　）
A．
-
1
2
B．
1
2
C．-2 D．2
组卷：135引用：5难度：0.7
解析
4．在三棱柱ABC-A₁B₁C₁中，
AB
=
a
，
AC
=
b
，
A
A
1
=
c
．点M在棱BC上，且BM=2MC，N为AA₁的中点，若以
a
，
b
，
c
为基底，则
MN
=（　　）
A．
-
2
3
a
-
1
3
b
+
1
2
c
B．
2
3
a
-
1
3
b
+
1
2
c
C．
-
1
3
a
+
2
3
b
-
1
2
c
D．
-
1
3
a
-
2
3
b
+
1
2
c
组卷：46引用：4难度：0.7
解析
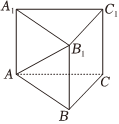5．如图，在正三棱柱ABC-A₁B₁C₁中，若AB=BB₁=2，则点C到直线AB₁的距离为（　　）
A．
14
B．
14
2
C．
14
3
D．
14
4
组卷：126引用：7难度：0.6
解析
6．已知直线l：λx-y-λ+1=0和圆C：x²+y²-4y=0交于A，B两点，则|AB|的最小值为（　　）
A．2 B．
2
C．4 D．
2
2
组卷：235引用：4难度：0.6
解析
7．已知底面为正方形的四棱锥P-ABCD的五个顶点在同一球面上，PD⊥BC，AB=4，
PC
=
2
，
PD
=
2
3
，则四棱锥P-ABCD外接球的表面积为（　　）
A．32π B．
8
2
π
3
C．36π D．24π
组卷：123引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共6小题，共70分）

21．如图1，等腰梯形AECD是由三个全等的等边三角形拼成，现将△BCE沿BC翻折至△BCP，使得
PD
=
3
2
AB
，如图2所示．

（1）求证：PD⊥BC；
（2）在直线PD上是否存在点M，使得直线BM与平面APD所成角的余弦值为
10
4
？若存在，求出
PM
DM
的值；若不存在，说明理由．
组卷：198引用：5难度：0.3
解析
22．在平面直角坐标系xOy中，已知原点O和点P（1，1），圆
C
：
（
x
-
3
2
）
2
+
（
y
+
1
2
）
2
=
5
2

（1）求圆C在x轴上截得的线段长度．
（2）若M，N为圆C上两点，若四边形MONP的对角线MN的方程为x+2y+m=0，求四边形MONP面积的最大值；
（3）过点P作两条相异直线分别与圆C相交于A，B两点，若直线PA，PB的斜率分别为k₁，k₂，且k₁+k₂=0，试判断直线AB的斜率是否为定值，并说明理由．
组卷：48引用：3难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．（x-3）²+（y-2）²=25	B．（x+3）²+（y+2）²=5
C．（x-3）²+（y-2）²=5	D．（x+3）²+（y+2）²=25

A． - 2 3 a - 1 3 b + 1 2 c	B． 2 3 a - 1 3 b + 1 2 c
C． - 1 3 a + 2 3 b - 1 2 c	D． - 1 3 a - 2 3 b + 1 2 c

2023-2024学年广东省广州市真光中学高二（上）期中数学试卷

一、单选题（本题共8小题，每小题5分，共40分）

1．已知A（1，1，1），B（3，3，3），O为坐标原点，求OA与BO的夹角（ ）

2．过点A（-6，2），B（2，-2）且圆心在直线x-y+1=0上的圆的方程是（ ）

3．已知直线：l1：y=ax+3与l2关于直线y=x对称，l2与l3：x+2y-1=0平行，则a=（ ）

4．在三棱柱ABC-A1B1C1中，AB=a，AC=b，AA1=c．点M在棱BC上，且BM=2MC，N为AA1的中点，若以a，b，c为基底，则MN=（ ）

5．如图，在正三棱柱ABC-A1B1C1中，若AB=BB1=2，则点C到直线AB1的距离为（ ）

6．已知直线l：λx-y-λ+1=0和圆C：x2+y2-4y=0交于A，B两点，则|AB|的最小值为（ ）

7．已知底面为正方形的四棱锥P-ABCD的五个顶点在同一球面上，PD⊥BC，AB=4，PC=2，PD=23，则四棱锥P-ABCD外接球的表面积为（ ）

四、解答题（本题共6小题，共70分）

1．已知A（1，1，1），B（3，3，3），O为坐标原点，求
OA
与
BO
的夹角（　　）

2．过点A（-6，2），B（2，-2）且圆心在直线x-y+1=0上的圆的方程是（　　）

3．已知直线：l₁：y=ax+3与l₂关于直线y=x对称，l₂与l₃：x+2y-1=0平行，则a=（　　）

4．在三棱柱ABC-A₁B₁C₁中，
AB
=
a
，
AC
=
b
，
A
A
1
=
c
．点M在棱BC上，且BM=2MC，N为AA₁的中点，若以
a
，
b
，
c
为基底，则
MN
=（　　）

5．如图，在正三棱柱ABC-A₁B₁C₁中，若AB=BB₁=2，则点C到直线AB₁的距离为（　　）

6．已知直线l：λx-y-λ+1=0和圆C：x²+y²-4y=0交于A，B两点，则|AB|的最小值为（　　）

7．已知底面为正方形的四棱锥P-ABCD的五个顶点在同一球面上，PD⊥BC，AB=4，
PC
=
2
，
PD
=
2
3
，则四棱锥P-ABCD外接球的表面积为（　　）