2021年四川省成都市公立名校（高中）自主招生数学试卷

一、选择题（本大题共9个小题。每小题6分，共54分）

• 1．无论k取何值时，关于x,y的方程（k-1）x+（k+1）y-k+3=0均有解

  x = m

  y = n

  ，则m²⁰¹⁵+n²⁰¹⁵的值为（　　）

  A．0

  B．-2

  C．22015-1

  D．-22015-1
  组卷：536引用：1难度：0.9

  解析

• 2．如图，A，B是反比例函数y=

  k

  x

  （k＞0）的图象上的两点，AC⊥x轴于点C，BD⊥y轴于点D，AC，BD交于点E，则△ADE与△BCE的面积关系是（　　）

  A．S△ADE＞S△BCE	B．S△ADE=S△BCE
  C．S△ADE＜S△BCE	D．不确定
  组卷：117引用：1难度：0.6

  解析

• 3．方程

  1

  x

  -2=x²-2x有（　　）个实数根．

  A．0

  B．1

  C．2

  D．3
  组卷：219引用：1难度：0.9

  解析

• 4．某纺织厂的一个车间有技术工人m名（m∈N*），编号分别为1，2，3，…，m,有n台（n∈N*）织布机，编号分别为1，2，3，…，n,定义记号a_ij：若第i名工人操作了第j号织布机，规定a_ij=1，否则a_ij=0，则等式a₄₁+a₄₂+a₄₃+…+a_4n=3的实际意义是（　　）

  A．第4名工人操作了3台织布机

  B．第4名工人操作了n台织布机

  C．第3名工人操作了4台织布机

  D．第3名工人操作了n台织布机
  组卷：75引用：1难度：0.5

  解析

• 5．已知

  x

  =

  1

  -

  a

  2

  ，

  x

  +

  a

  -

  x

  -

  a

  +

  2

  =-2，则a的取值范围是（　　）

  A．a≤1

  B．-1≤a≤1

  C．a≤-1

  D．-1≤a≤0
  组卷：363引用：1难度：0.9

  解析

• 6．一个三角形的边长分别为a,a,b,另一个三角形的边长分别为b,b,a,其中a＞b,若两个三角形的最小内角相等，

  a

  b

  的值等于（　　）

  A． 3 + 1 2

  B． 5 + 1 2

  C． 3 + 2 2

  D． 5 + 2 2
  组卷：2264引用：9难度：0.5

  解析

三、解答题（本大题头5个小题，72分）

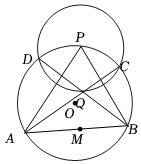• 17．如图，已知AB为⊙O的弦，点M为AB的中点，P为⊙O上任意一点，以点P为圆心、2MO为半径作圆交⊙O于C，D两点，AC，BD交于点Q．
  （1）求证：点Q是△PAB的垂心；
  （2）判断点Q是否在⊙P上，并证明你的结论．
  组卷：175引用：1难度：0.5

  解析

• 18．已知二次函数y=ax²+bx+c（0＜a＜1）的最小值为1，且直线y=x-

  3

  4

  与二次函数图象的两个交点的横坐标分别为2和4．
  （1）求二次函数的表达式．
  （2）如图1，以点H（1，h）（h＞

  3

  2

  ）为圆心，

  1

  2

  为半径作圆，抛物线y=ax²+bx+c上仅有唯一点J，使得过点J向⊙H作切线的切线段JK长度最小，求h的取值范围．
  （3）如图2，过定点F（1，2）的直线y=kx-k+2（k＞0）与抛物线y=ax²+bx+c交于A、B两个不同点，与x轴交于R点，令θ=∠ARO（O为坐标原点．
  （i）判断以A为圆心，AF为半径的圆与x轴的位置关系，并加以证明．
  （ii）cosθ为何值时，x轴上存在点Q，使得△ABQ为等边三角形，并求出此时△ABQ的面积．
  
  组卷：125引用：1难度：0.2

  解析