2023-2024学年北京市门头沟区大峪中学高二（上）期中数学试卷

一、选择题（本大题共10小题，每题4分，共40分）

• 1．已知直线

  l

  ：

  3

  x

  -

  y

  -

  4

  =

  0

  ，则直线l的倾斜角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：195引用：5难度：0.8

  解析

• 2．已知空间向量

  a

  =

  （

  0

  ，

  2

  ，

  0

  ）

  ，

  b

  =

  （

  1

  ，

  0

  ，-

  1

  ）

  ，则

  （

  a

  +

  b

  ）

  •

  b

  =（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：65引用：3难度：0.8

  解析

• 3．圆x²+y²-2x+4y+1=0与圆（x-4）²+（y-2）²=16的位置关系为（　　）

  A．相离

  B．外切

  C．相交

  D．内切
  组卷：81引用：3难度：0.7

  解析

• 4．若x²+y²-4x-2y+m=0表示圆的方程，则m的取值范围是（　　）

  A．（-∞，5）

  B．（-∞，5]

  C．（5，+∞）

  D．[5，+∞）
  组卷：90引用：3难度：0.9

  解析

• 5．已知直线x+ay-1=0和直线ax+4y+2=0互相平行，则a的值是（　　）

  A．0

  B．2

  C．-2

  D．±2
  组卷：106引用：4难度：0.7

  解析

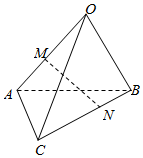• 6．如图，空间四边形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，点M是OA的中点，点N在BC上，且

  CN

  =2

  NB

  ，设

  MN

  =x

  a

  +y

  b

  +z

  c

  ，则x,y,z的值为（　　）

  A． 1 2 ， 1 3 ， 2 3

  B． 1 2 ， 2 3 ， 1 3

  C．- 1 2 ， 2 3 ， 1 3

  D．- 1 2 ， 1 3 ， 2 3
  组卷：617引用：21难度：0.8

  解析

• 7．点（-1，2）关于直线x+y+4=0的对称点的坐标为（　　）

  A．（-6，-3）

  B．（-3，-6）

  C．（-7，-2）

  D．（-2，-7）
  组卷：137引用：2难度：0.7

  解析

三、解答题（共6小题，共85分.解答应写出文字说明、证明过程或演算步骤）

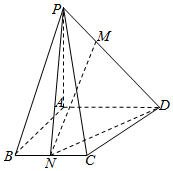• 20．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，其中AD∥BC，AD⊥BA，AD=3，AB=BC=2，PA⊥平面ABCD，且PA=3，点M在棱PD上，点N为BC中点．
  （1）证明：若DM=2MP，直线MN∥平面PAB；
  （2）求二面角C-PD-N的正弦值；
  （3）是否存在点M，使NM与平面PCD所成角的正弦值为

  2

  6

  ？若存在求出

  PM

  PD

  值；若不存在，说明理由．
  组卷：600引用：10难度：0.6

  解析

• 21．对于平面直角坐标系中的两点A（x₁，y₁），B（x₂，y₂），现定义由点A到点B的“折线距离”ρ（A，B）为ρ（A，B）=|x₂-x₁|+|y₂-y₁|．
  （1）已知A（1，0），B（2，3），求ρ（A，B）；
  （2）已知点A（1，0），点B是直线

  l

  ：

  x

  -

  2

  y

  +

  2

  =

  0

  上的一个动点，求ρ（A，B）的最小值；
  （3）对平面上给定的两个不同的点A（x₁，y₁），B（x₂，y₂），是否存在点C（x,y），同时满足
  ①ρ（A，C）+ρ（C，B）=ρ（A，B）；②ρ（A，C）=ρ（C，B）．
  若存在，请求出所有符合条件的点；若不存在，请予以证明．
  组卷：32引用：3难度：0.5

  解析