2023-2024学年广东省东莞中学高二(上)第一次段考数学试卷
发布:2024/9/20 2:0:8
一、选择愿(每小题5分,共60分)
-
1.已知圆心为(-2,1)的圆与y轴相切,则该圆的标准方程是( )
组卷:428引用:7难度:0.8 -
2.已知
是不共面的三个向量,则能构成空间的一个基底的一组向量是( )a,b,c组卷:131引用:5难度:0.8 -
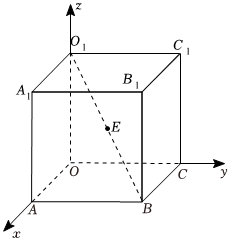 3.如图,正方体OABC-O1A1B1C1的棱长为3,E是线段O1B上的点,且2EB=EO1,则点E的坐标为( )组卷:52引用:5难度:0.7
3.如图,正方体OABC-O1A1B1C1的棱长为3,E是线段O1B上的点,且2EB=EO1,则点E的坐标为( )组卷:52引用:5难度:0.7 -
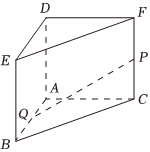 4.如图,在三棱柱ABC-DEF中,P,Q分别是CF,AB的中点,,则a+b+c=( )PQ=aAB+bAC+cAD组卷:210引用:4难度:0.7
4.如图,在三棱柱ABC-DEF中,P,Q分别是CF,AB的中点,,则a+b+c=( )PQ=aAB+bAC+cAD组卷:210引用:4难度:0.7 -
5.已知空间向量
满足m、n,则|m|=2,|n|=3,|m-n|=17在m上的投影向量( )n组卷:109引用:1难度:0.8 -
6.设m∈R,过定点A的直线x+my-m=0和过定点B的直线mx-y-m+3=0交于点P,则|PA|2+|PB|2的值为( )
组卷:139引用:1难度:0.5 -
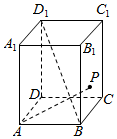 7.如图,在正四棱柱ABCD-A1B1C1D1中,AB=3,AA1=4,P是侧面BCC1B1内的动点,且AP⊥BD1,记AP与平面BCC1B所成的角为θ,则tanθ的最大值为( )组卷:434引用:13难度:0.6
7.如图,在正四棱柱ABCD-A1B1C1D1中,AB=3,AA1=4,P是侧面BCC1B1内的动点,且AP⊥BD1,记AP与平面BCC1B所成的角为θ,则tanθ的最大值为( )组卷:434引用:13难度:0.6
三、解答题(第17题10分,其余5题得小题12分,共70分)
-
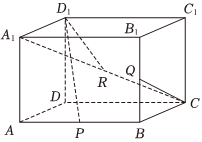 21.在长方体ABCD-A1B1C1D1中,AD=AA1=2.R是线段A1C上的点.
21.在长方体ABCD-A1B1C1D1中,AD=AA1=2.R是线段A1C上的点.
(1)若,求证:D1R∥平面BDC1.A1R=13A1C
(2)若,在线段BB1上是否存在点Q.使D1R⊥CQ,若存在,求λ的取值范围;若不存在,请说明理由.A1R=λA1C组卷:28引用:1难度:0.5 -
22.如图1,梯形ABCD中,AB∥CD,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E,F,AB=AE=2,CD=5,已知DE=1,将梯形ABCD沿AE、BF折起,得空间几何体ADE-BCF,如图2.
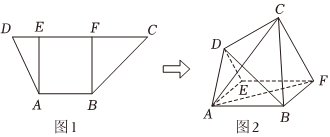
(1)在图2中,若AF⊥BD,证明:DE⊥平面ABFE.
(2)在图2中,若DE∥CF,CD=,在线段AB上求一点P,使CP与平面ACD所成角的正弦值最大,并求出这个最大值.3组卷:66引用:3难度:0.5


