2023年湖南省高考数学模拟试卷（三）

一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合

  A

  =

  {

  x

  |

  y

  =

  4

  x

  -

  x

  2

  }

  ，B={x|1-x＞0}，则A∪B=（　　）

  A．{x|0≤x＜1}

  B．{x|x≤4}

  C．{x|1＜x≤4}

  D．{x|x≥0}
  组卷：162引用：6难度：0.9

  解析

• 2．已知复数z₁，z₂是方程x²+x+1=0的两个根，则

  z

  2

  z

  1

  +

  1

  +

  z

  1

  z

  2

  +

  1

  =（　　）

  A．-1

  B．1

  C．-2

  D．0
  组卷：102引用：2难度：0.7

  解析

• 3．设正项等比数列{a_n}的前n项和为S_n，若2S₃=3a₂+8a₁，S₈=2S₇+2，则a₂=（　　）

  A．4

  B．3

  C．2

  D．1
  组卷：790引用：8难度：0.5

  解析

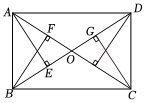• 4．、2000多年前，古希腊雅典学派的第三大算学家欧道克萨斯首先提出黄金分割，所谓黄金分割点，指的是把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比，黄金分割比为

  5

  -

  1

  2

  ，如图，在矩形ABCD中，AC与BD相交于点O，BF⊥AC，DH⊥AC，AE⊥BD，CG⊥BD，且点E为线段BO的黄金分割点，则

  BF

  =（　　）、

  A． 3 - 5 2 BA + 5 + 5 10 BG	B． 3 - 5 2 BA + 5 - 5 10 BG
  C． 5 - 1 2 BA + 5 - 5 10 BG	D． 3 - 5 2 BA + 5 5 BG
  组卷：71引用：3难度：0.6

  解析

• 5．已知：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的任何平面所截，如果截得两个截面的面积之比为k（常数），那么这两个几何体的体积之比也为k,则椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）绕长轴旋转一周形成的几何体的体积为（　　）

  A． 4 3 π a 2 b

  B． 4 3 π a b 2

  C． 4 3 π a 3

  D． 4 3 π b 3
  组卷：81引用：3难度：0.5

  解析

• 6．2021年春节联欢晚会以“共圆小康梦，欢乐过大年”为主题，突出时代性、人民性、创新性，节目内容丰富多彩，呈现形式新颖多样，某小区的5个家庭买了8张连号的门票，其中甲家庭需要3张连号的门票、乙家庭需要2张连号的门票，剩余的3张随机分到剩余的3个家庭即可，则这8张门票分配到家庭的不同方法种数为（　　）

  A．48

  B．72

  C．120

  D．240
  组卷：105引用：3难度：0.6

  解析

• 7．若a=ln1.01，b=

  2

  201

  ，

  c

  =

  1

  .

  02

  -1，则（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．b＜c＜a

  D．c＜a＜b
  组卷：295引用：6难度：0.4

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.

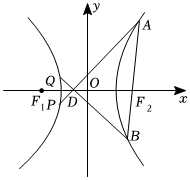• 21．如图，在平面直角坐标系中，F₁，F₂分别为等轴双曲线Γ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦点，若点A为双曲线右支上一点，且|AF₁|-|AF₂|=4

  2

  ，直线AF₂交双曲线于B点，点D为线段F₁O的中点，延长AD，BD，分别与双曲线Γ交于P，Q点．
  （1）若A（x₁，y₁），B（x₂，y₂），求证：x₁y₂-x₂y₁=4（y₂-y₁）；
  （2）若直线AB，PQ的斜率都存在，且依次设为k₁，k₂，试判断

  k

  2

  k

  1

  是否为定值，如果是，请求出

  k

  2

  k

  1

  的值；如果不是，请说明理由．
  组卷：91引用：1难度：0.3

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  a

  e

  x

  x

  +

  lnx

  -

  x

  （a＞0）．
  （1）若a=1，讨论f（x）的单调性；
  （2）若函数f（x）存在两个极小值点x₁，x₂，求实数a的取值范围；
  （3）当a＞1时，设

  F

  （

  x

  ）

  =

  f

  （

  x

  ）

  -

  （

  2

  lnx

  -

  x

  +

  1

  x

  ）

  ，求证：

  F

  （

  x

  ）

  ≥

  ln

  （

  ax

  ）

  x

  -

  lnx

  +

  e

  -

  1

  ．
  组卷：344引用：5难度：0.2

  解析