2022-2023学年浙江省台州市临海市大田中学八年级（上）第一次统练数学试卷（10月份）

一．选择题（共10小题，每小题4分，共40分）

• 1．下列图形中具有稳定性的是（　　）

  A．三角形

  B．长方形

  C．正方形

  D．平行四边形
  组卷：177引用：17难度：0.7

  解析

• 2．画△ABC中AC边上的高，下列四个画法中正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：3369引用：49难度：0.9

  解析

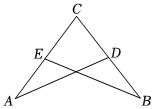• 3．如图，已知△CAD≌△CBE，若∠A=30°，∠C=70°，则∠CEB=（　　）

  A．50°

  B．60°

  C．70°

  D．80°
  组卷：324引用：9难度：0.6

  解析

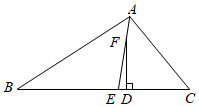• 4．△ABC中，∠C=50°，∠B=30°，AE平分∠BAC，点F为AE上一点，FD⊥BC于点D，则∠EFD的度数为（　　）

  A．5°

  B．10°

  C．12°

  D．20°
  组卷：871引用：10难度：0.8

  解析

• 5．如图，小颖按下面方法用尺规作角平分线：在已知的∠AOB的两边上，分别截取OC，OD，使OC=OD．再分别以点C，D为圆心、大于

  1

  2

  CD

  的长为半径作弧，两弧在∠AOB内交于点P，作射线OP，则射线OP就是∠AOB的平分线．其作图原理是：△OCP≌△ODP，这样就有∠AOP=∠BOP，那么判定这两个三角形全等的依据是（　　）

  A．SAS

  B．ASA

  C．AAS

  D．SSS
  组卷：563引用：9难度：0.5

  解析

• 6．设三角形三边之长分别为2，9，5+a,则a的取值范围为（　　）

  A．2＜a＜9

  B．7＜a＜11

  C．7＜a＜9

  D．2＜a＜6
  组卷：31引用：3难度：0.6

  解析

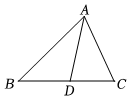• 7．如图，在△ABC中，AB=20，AC=18，AD为中线．则△ABD与△ACD的周长之差为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：1220引用：3难度：0.7

  解析

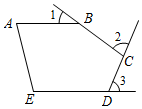• 8．如图，在五边形ABCDE中，AB∥ED，∠1，∠2，∠3分别是∠ABC，∠BCD，∠CDE的外角，则∠1+∠2+∠3的度数为（　　）

  A．180°

  B．210°

  C．240°

  D．270°
  组卷：1321引用：12难度：0.5

  解析

三、解答题（本题共8小题，共80分。）

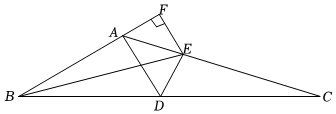• 23．如图，在△ABC中，点D在BC边上，∠BAD=100°，∠ABC的平分线交AC于点E，过点E作EF⊥AB，垂足为F，且∠AEF=50°，连接DE．
  （1）求∠CAD的度数；
  （2）求证：DE平分∠ADC；
  （3）若AB=6，AD=4，CD=8，且S_△ACD=18，求△ABE的面积．
  组卷：354引用：1难度：0.5

  解析

• 24．（1）阅读理解：如图①，在△ABC中，若AB=15，AC=9，求BC边上的中线AD的取值范围．
  解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB、AC，2AD集中在△ABE中，利用三角形三边的关系即可判断中线AD的取值范围是

  ；
  （2）问题解决：如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；
  （3）问题拓展：如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=120°，以C为顶点作一个60°角，角的两边分别交AB，AD于E、F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．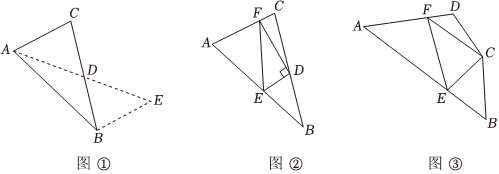
  
  组卷：152引用：1难度：0.3

  解析