当前位置：试卷中心 > 试卷详情

2022-2023学年上海市杨浦区控江中学高一（下）期末数学试卷

发布：2024/6/18 8:0:10

一、填空题（本大题满分54分）本大概共有12题，1～6题每题4分，7～12题每题5分.

1．半径为2，弧长为2的扇形的圆心角为
弧度．
组卷：82引用：1难度：0.9
解析
2．函数y=tanx的最小正周期是
．
组卷：294引用：4难度：0.8
解析
3．向量
b
=（3，4）的单位向量
b
0
为
．
组卷：83引用：1难度：0.9
解析
4．若角α的终边过点P（4，-3），则
sin
（
3
π
2
+
α
）
=
．
组卷：1210引用：10难度：0.9
解析
5．已知复数z=1+2i,则z•
z
=
．
组卷：190引用：8难度：0.7
解析
6．已知直角坐标平面上两点P₁（-1，1）、P₂（2，3），若P满足
P
1
P
=
2
P
P
2
，则点P的坐标为
．
组卷：101引用：1难度：0.7
解析
7．在△ABC中，角A，B，C所对的边为a,b,c,若a=4，b=6，c=9，则角C=
．
组卷：280引用：2难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、简答题（本大题满分78分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必得步骤.

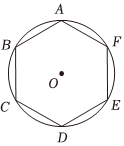20．如图，设ABCDEF是半径为1的圆O的内接正六边形，M是圆O上的动点．
（1）求
|
AB
+
BC
-
AM
|
的最大值；
（2）求证：
MA
2
+
MD
2
为定值；
（3）对于平面中的点P，存在实数x与y,使得
OP
=
x
OE
+
y
OF
，若点P是正六边形ABCDEF内的动点（包含边界），求x-y的最小值．
组卷：106引用：1难度：0.6
解析
21．设f（z）是一个关于复数z的表达式，若f（x+yi）=x₁+y₁i（其中x,y,x₁，y₁∈R，i为虚数单位），就称f将点P（x,y）“f对应”到点Q（x₁，y₁）．例如：
f
（
z
）
=
1
z
将点（0，1）“f对应”到点（0，-1）．
（1）若f（z）=z+1（z∈C），点P₁（1，1）“f对应”到点Q₁，点P₂“对应”到点Q₂（1，1），求点Q₁、P₂的坐标．
（2）设常数k,t∈R，若直线l：y=kx+t,f（z）=z²（z∈C），是否存在一个有序实数对（k,t），使得直线l上的任意一点P（x,y）“f对应”到点Q（x₁，y₁）后，点Q仍在直线l上？若存在，试求出所有的有序实数对（k,t）；若不存在，请说明理由．
（3）设常数a,b∈R，集合D{z|z∈C且Rez＞0}和A={w|w∈C且|w|＜1}，若
f
（
z
）
=
az
+
b
z
+
1
满足：①对于集合D中的任意一个元素z,都有f（z）∈A；②对于集合A中的任意一个元素w,都存在集合D中的元素z使得w=f（z）．请写出满足条件的一个有序实数对（a,b），并论证此时的f（z）满足条件．
组卷：68引用：6难度：0.3
解析