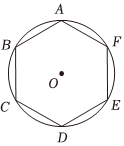
如图，设ABCDEF是半径为1的圆O的内接正六边形，M是圆O上的动点．
（1）求|AB+BC-AM|的最大值；
（2）求证：MA2+MD2为定值；
（3）对于平面中的点P，存在实数x与y,使得OP=xOE+yOF，若点P是正六边形ABCDEF内的动点（包含边界），求x-y的最小值．
|
AB
+
BC
-
AM
|
MA
2
+
MD
2
OP
=
x
OE
+
y
OF
【考点】平面向量的基本定理．
【答案】（1）2；
（2）4；
（3）-2．
（2）4；
（3）-2．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/28 8:0:9组卷：106引用：1难度：0.6
