2022-2023学年河南省开封市通许县等3地高二（下）期末数学试卷
发布：2024/5/23 8:0:8
一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．设集合A={x|log2（x+2）＜2}，集合B={x|1≤2x≤8}，则A∩B=（ ）
组卷：103引用：3难度：0.8 -
2．已知命题p：∀x∈R，
，则￢p为（ ）sinx+cosx≥2组卷：34引用：3难度：0.8 -
3．已知关于x的不等式x2-4ax+3a2＜0（a＜0）的解集为（x1，x2），则
的最大值是（ ）x1+x2+ax1x2组卷：1244引用：35难度：0.9 -
4．第19届亚运会即将在西子湖畔——杭州召开，为了办好这一届“中国特色、浙江风采、杭州韵味、精彩纷呈”的体育文化盛会，杭州亚运会组委会决定进行赛会志愿者招募，在杭大学生纷纷踊跃参加．现有4名大学生志愿者，通过培训后，拟安排在游泳、篮球、体操三个项目进行志愿者服务，假设每个项目至少安排一名志愿者，且每位志愿者只能参与其中一个项目，在甲被安排到游泳项目的条件下，乙也被安排到游泳项目的概率为（ ）
组卷：85引用：2难度：0.7 -
5．设（3x-2）100=a0+a1x+a2x2+⋯+a100x100，若a0+a2+a4+…+a100+m=12k（k∈Z）．则实数m可能是（ ）
组卷：70引用：2难度：0.6 -
6．为研究变量x,y的相关关系，收集得到下列五个样本点（x,y）：
若由最小二乘法求得y关于x的回归直线方程为x 5 6.5 7 8 8.5 y 3 4 6 8 9 ，则据此计算残差为0的样本点是（ ）̂y=1.8x+̂a组卷：8引用：3难度：0.6 -
7．用四种颜色给正四棱锥V-ABCD的五个顶点涂色，要求每个顶点涂一种颜色，且每条棱的两个顶点涂不同颜色，则不同的涂法有（ ）
组卷：456引用：9难度：0.7
四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.
-
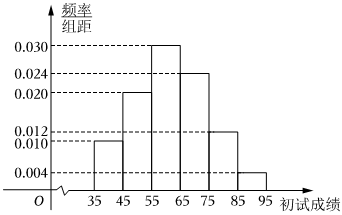21．某校数学组老师为了解学生数学学科核心素养整体发展水平，组织本校8000名学生进行针对性检测（检测分为初试和复试），并随机抽取了100名学生的初试成绩，绘制了频率分布直方图，如图所示．
（1）根据频率分布直方图，求样本平均数的估计值；
（2）若所有学生的初试成绩X近似服从正态分布N（μ，σ2），其中μ为样本平均数的估计值，σ≈14．初试成绩不低于90分的学生才能参加复试，试估计能参加复试的人数；
（3）复试共三道题，规定：全部答对获得一等奖；答对两道题获得二等奖；答对一道题获得三等奖；全部答错不获奖．已知某学生进入了复试，他在复试中前两道题答对的概率均为a,第三道题答对的概率为b.若他获得一等奖的概率为，设他获得二等奖的概率为P，求P的最小值．18
附：若随机变量X服从正态分布N（μ，σ2），则P（μ-σ＜X≤μ+σ）≈0.6827，P（μ-2σ＜X≤μ+2σ）≈0.9545，P（μ-3σ＜X≤μ+3σ）≈0.9973．组卷：689引用：12难度：0.6 -
22．已知函数f（x）=（a+1）ex+
-3，其中e为自然对数的底数，a∈R．aex
（1）讨论函数f（x）的单调性；
（2）当a=0时，若存在x∈R使得关于x的不等式k≥xf（x）成立，求k的最小整数值．（参考数据：≈2.1）e34组卷：27引用：1难度：0.2
