当前位置：试卷中心 > 试卷详情

2022-2023学年上海中学高一（下）期末数学试卷

发布：2024/5/30 8:0:9

一、填空题（每题3分，共36分）

1．已知复数z=1-2i（i为虚数单位），则Rez-Imz=
．
组卷：62引用：3难度：0.8
解析
2．已知点A（2，3），B（6，-3），若点P满足
AB
=
3
AP
，则点P的坐标为
．
组卷：78引用：2难度：0.8
解析
3．已知复数z满足z（1+2i）=3+4i（i为虚数单位），则|z|=
．
组卷：80引用：3难度：0.9
解析
4．设非零向量
a
，
b
满足|
a
|=|
b
|，且（2
a
+
b
）⊥
b
，则
a
与
b
的夹角为
．
组卷：129引用：10难度：0.7
解析
5．在正方体ABCD-A₁B₁C₁D₁中，AC与BD交于点O，则直线BC₁与直线OD₁的夹角为
．
组卷：74引用：3难度：0.6
解析
6．已知复平面上平行四边形ABCD的顶点A（-2，-1），B（7，3）、C（12，9）、D（x,y）按逆时针方向排列，则向量
AD
所对应的复数为
．
组卷：40引用：1难度：0.8
解析
7．设f（n）=
（
1
+
i
1
-
i
）
n
+
（
1
-
i
1
+
i
）
n
（
n
∈
N
）
，则集合{x|x=f（n）}的子集个数是
．
组卷：106引用：2难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共有5题，共48分，解答时必须写出必要的步骤）

20．利用平面向量的坐标表示，可以把平面向量的概念推广为坐标为复数的“复向量”，即可将有序复数对（z₁，z₂）（其中z₁，z₂∈C）视为一个向量，记作
α
=
（
z
1
，
z
2
）
．类比平面向量可以定义其运算，两个复向量
α
=
（
z
1
，
z
2
）
，
β
=
（
z
1
′，
z
2
′
）
的数量积定义为一个复数，记作
a
•
β
，满足
α
•
β
=
z
1
z
1
′
+
z
2
z
2
′
，复向量
α
的模定义为
|
α
|
=
α
•
α
′
．
（1）设
α
=
（
1
-
i
,
i
）
，
β
=（3，4），i为虚数单位，求复向量
α
、
β
的模；
（2）设
α
、
β
是两个复向量．
①已知对于任意两个平面向量
a
=
（
x
1
，
y
1
）
，
b
=
（
x
2
，
y
2
）
，（其中x₁，x₂，y₁，y₂∈R），
|
a
•
b
|
≤
|
a
|
|
b
|
成立，证明：对于复向量
α
、
β
，
|
α
•
β
|
≤
|
α
|
|
β
|
也成立；
②当
|
α
•
β
|
=
|
α
|
|
β
|
时，称复向量
α
与
β
平行．若复向量
α
=
（
1
+
i
,
1
-
2
i
）
与
β
=（i,z）平行（其中i为虚数单位，z∈C），求复数z.
组卷：236引用：3难度：0.3
解析
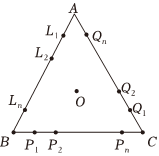21．如图，已知O是边长为1的正△ABC的外心，P₁，P₂，…，P_n为BC边上的n+1等分点，Q₁，Q₂，…，Q_n为AC边上的n+1等分点，L₁，L₂，…，L_n为AB边上的n+1等分点．
（1）当n=2023时，求|
OC
+
O
P
1
+
O
P
2
+
…
+
O
P
2023
+
OB
|的值；
（2）当n=4时．
①求
OA
•
A
Q
j
+
OA
•
A
L
k
的值（用含j,k的式子表示）；
②若M={m|m=
O
P
i
•
O
Q
j
+
O
Q
j
•
O
L
k
+
O
L
k
•
O
P
i
，1≤i,j,k≤4，i,j,k∈N}，分别求集合M中最大元素与最小元素的值．

组卷：110引用：2难度：0.2
解析