2023-2024学年四川省宜宾四中高二(上)开学数学试卷
发布:2024/8/12 2:0:1
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.设集合A={x||x-2|<2},B={x|x2-3x+2<0},若U=R,则A∩∁UB=( )
组卷:33引用:2难度:0.7 -
2.若x>0,y>0,且
,则4x+2y的最小值为( )1x+1+1x+2y=1组卷:922引用:3难度:0.6 -
3.函数
的图象和函数f(x)=4x-4,x≤1x2-6x+5,x>1的图象的交点的个数为( )g(x)=log15(x+2)组卷:56引用:1难度:0.5 -
4.若
,cos(α-β)=-12,则cos(π-α)cos(π+β)=( )cos(α+β)=14组卷:332引用:5难度:0.9 -
5.18世纪末期,挪威测量学家威塞尔首次利用坐标平面上的点来表示复数,使复数及其运算具有了几何意义.例如,|z|=|OZ|,即复数z的模的几何意义为z在复平面内对应的点Z到原点的距离.在复平面内,若复数
对应的点为Z1,Z为曲线|z-3|=1上的动点,则Z1与Z之间的最小距离为( )z1=-4-4i1-i组卷:150引用:4难度:0.7 -
6.已知函数y=sinx的定义域为[a,b],值域为[-1,
],则b-a的最大值和最小值之差等于( )32组卷:84引用:3难度:0.6 -
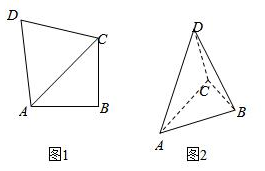 7.如图,在四边形ABCD中,AB=BC=2,∠ABC=90°,DA=DC=.现沿对角线AC折起,使得平面DAC⊥平面ABC,此时点A,B,C,D在同一个球面上,则该球的体积是( )6组卷:467引用:6难度:0.7
7.如图,在四边形ABCD中,AB=BC=2,∠ABC=90°,DA=DC=.现沿对角线AC折起,使得平面DAC⊥平面ABC,此时点A,B,C,D在同一个球面上,则该球的体积是( )6组卷:467引用:6难度:0.7
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知函数
是定义在R上的奇函数.f(x)=m-ex1+ex
(1)求函数f(x)的解析式,判断并证明函数y=f(x)的单调性;
(2)若存在实数t∈[1,4],使f(t2+2t+k)+f(-2t2+2t-5)>0成立,求实数k的取值范围.组卷:154引用:3难度:0.6 -
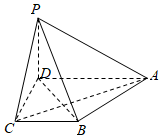 22.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=.平面PAD⊥平面ABCD,∠PDA=90°.2
22.如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,CD=.平面PAD⊥平面ABCD,∠PDA=90°.2
(1)若平面PAD∩平面PBC=l,求证:l∥BC;
(2)求证:平面PAC⊥平面PBD;
(3)若二面角B-PA-D的正切值为2,求四棱锥P-ABCD的体积.2组卷:732引用:5难度:0.5


