2023-2024学年陕西省西安市鄠邑区高二（上）期中数学试卷

一、单项选择题（本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．过点（1，0）且与直线x-2y-2=0平行的直线方程是（　　）

  A．x-2y-1=0

  B．x-2y+1=0

  C．2x+y-2=0

  D．x+2y-1=0
  组卷：4701引用：156难度：0.9

  解析

• 2．设m∈R，则直线l：mx+y-m-1=0与圆x²+y²=2的位置关系为（　　）

  A．相离

  B．相切

  C．相交或相切

  D．相交
  组卷：62引用：4难度：0.7

  解析

• 3．在空间直角坐标系Oxyz中，点A（2，3，6）在坐标平面Oxz内的射影为点B，则B的坐标为（　　）

  A．（0，3，6）

  B．（2，0，6）

  C．（2，3，0）

  D．（2，0，3）
  组卷：48引用：10难度：0.8

  解析

• 4．从圆x²-2x+y²-2y+1=0外一点P（3，2）向这个圆作两条切线，则两切线夹角的余弦值为（　　）

  A． 1 2

  B． 3 5

  C． 3 2

  D．0
  组卷：2189引用：30难度：0.9

  解析

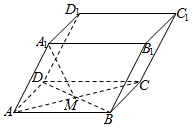• 5．如图，在平行六面体ABCD-A₁B₁C₁D₁中，AC与BD交点为M．设

  A

  1

  B

  1

  =

  a

  ，

  A

  1

  D

  1

  =

  b

  ，

  A

  1

  A

  =

  c

  ，则下列向量中与

  2

  A

  1

  M

  相等的向量是（　　）

  A． a + b + 2 c

  B． - a + b + 2 c

  C． a - b + 2 c

  D． - a - b + 2 c
  组卷：171引用：2难度：0.8

  解析

• 6．唐代诗人李顾的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河”，诗中隐含着一个有趣的数学问题--“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在的位置为A（1，1），若将军从山脚下的点B（4，4）处出发，河岸线所在直线l的方程为x-y+1=0，则“将军饮马”的最短总路程是（　　）

  A．3 6

  B． 34

  C． 5

  D．2 5
  组卷：223引用：4难度：0.7

  解析

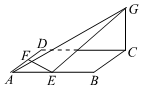• 7．如图，已知正方形ABCD的边长为4，E，F分别是AB，AD的中点，GC⊥平面ABCD，且GC=2，则点B到平面EFG的距离为（　　）

  A． 10 10

  B． 2 11 11

  C． 3 5

  D．1
  组卷：55引用：3难度：0.5

  解析

四、解答题（本大题共6个小题，共70分.解答应写出文字说明、证明过程或演算步骤）

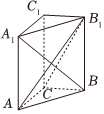• 21．如图，在直三棱柱ABC-A₁B₁C₁中，已知CA=CB=1，AA₁=2，∠BCA=90°．
  （1）求异面直线BA₁与CB₁夹角的余弦值；
  （2）求二面角B-AB₁-C平面角的余弦值．
  组卷：134引用：4难度：0.3

  解析

• 22．公元前3世纪，古希腊数学家阿波罗尼斯在《平面轨迹》一书中，曾研究了众多的平面轨迹问题，其中有如下结果：平面内到两定点距离之比等于已知数的动点轨迹为直线或圆，后世把这种圆称之为阿波罗尼斯圆．已知平面直角坐标系中A（-2，0），B（1，0）且|PA|=2|PB|．
  （1）求点P的轨迹方程；
  （2）若点P在（1）的轨迹上运动，点M为AP的中点，求点M的轨迹方程；
  （3）若点P（x,y）在（1）的轨迹上运动，求

  t

  =

  y

  +

  4

  x

  -

  6

  的取值范围．
  组卷：81引用：7难度：0.5

  解析