2022-2023学年浙江省精诚联盟高二(下)联考数学试卷(3月份)
发布:2024/7/12 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知
,a=(2,0,2)分别是平面α,β的法向量,则平面α,β交线的方向向量可以是( )b=(3,0,0)组卷:173引用:5难度:0.7 -
2.已知双曲线
的两条渐近线的夹角为x2a2-y23=1,则双曲线的焦点到渐近线的距离是( )π3组卷:113引用:3难度:0.7 -
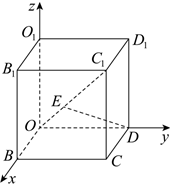 3.如图,在空间直角坐标系Oxyz中,正方体OBCD-O1B1C1D1的棱长为1,且DE⊥OC1于点E则=( )OE组卷:178引用:2难度:0.8
3.如图,在空间直角坐标系Oxyz中,正方体OBCD-O1B1C1D1的棱长为1,且DE⊥OC1于点E则=( )OE组卷:178引用:2难度:0.8 -
4.若点A(a,a),B(b,eb)(a,b∈R),则A、B两点间距离|AB|的最小值为( )
组卷:95引用:2难度:0.6 -
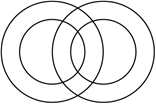 5.如图,4个圆相交共有8个交点,现在4种不同的颜色供选用,给8个交点染色,要求在同一圆上的4个交点的颜色互不相同,则不同的染色方案共有( )种.组卷:216引用:3难度:0.5
5.如图,4个圆相交共有8个交点,现在4种不同的颜色供选用,给8个交点染色,要求在同一圆上的4个交点的颜色互不相同,则不同的染色方案共有( )种.组卷:216引用:3难度:0.5 -
6.已知直线l:x-y-2=0与抛物线E:y2=2x交于A、B两点,抛物线E分别在点A、B处的两条切线交于点P,则点P在直线l上的投影的坐标为( )
组卷:36引用:2难度:0.5 -
7.已知递增数列{an}的前n项和Sn满足2Sn=n(an+1),n∈N*,设
,若对任意n∈N*,不等式bn=1ana2n+1-an+1a2n恒成立,则a2023的最小值为( )b1+b2+b3+…+bn≤14组卷:86引用:2难度:0.4
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
-
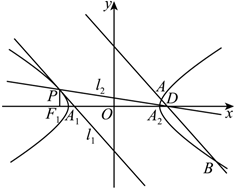 21.已知曲线,焦点F1,F2,C:x23-y2b2=1,A1(-3,0),P是左支上任意一点(异于点A1),且直线PA1与PA2的斜率之积为A2(3,0).13
21.已知曲线,焦点F1,F2,C:x23-y2b2=1,A1(-3,0),P是左支上任意一点(异于点A1),且直线PA1与PA2的斜率之积为A2(3,0).13
(1)求曲线C的方程;
(2)直线l1为过P点的切线,直线l2与直线PF1关于直线l1对称,直线l2与x轴的交点D,过点D作直线l1的平行线与曲线C交于A,B两点,求△PAB面积的取值范围.组卷:37引用:2难度:0.5 -
22.已知函数f(x)=x(1-lnx).
(1)求f(x)的单调区间;
(2)设a,b为两个不相等的正数,且blna-alnb=a-b,证明:.2<1a+1b<e组卷:80引用:2难度:0.6


