2022-2023学年四川省德阳市什邡中学高一（下）第一次月考数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设集合A={x|-2＜x＜4}，B={2，3，4，5}，则A∩B=（　　）

  A．{2，3，4}

  B．{3，4}

  C．{2，3}

  D．{2}
  组卷：2154引用：53难度：0.8

  解析

• 2．命题“∃x＞0，x²-1＞0”的否定是（　　）

  A．∃x≤0，x2-1＞0	B．∃x＞0，x2-1≤0
  C．∀x＞0，x2-1≤0	D．∀x≤0，x2-1＞0
  组卷：78引用：5难度：0.7

  解析

• 3．计算cos（-600°）的结果是（　　）

  A． 3 2

  B．- 3 2

  C．- 1 2

  D． 1 2
  组卷：198引用：7难度：0.9

  解析

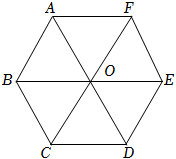• 4．如图所示，点O是正六边形ABCDEF的中心，则以图中点A、B、C、D、E、F、O中的任意一点为始点，与始点不同的另一点为终点的所有向量中，除向量

  OA

  外，与向量

  OA

  共线的向量共有（　　）

  A．6个

  B．7个

  C．8个

  D．9个
  组卷：386引用：7难度：0.7

  解析

• 5．在边长为1的正三角形ABC中，|

  AB

  -

  BC

  |的值为（　　）

  A．1

  B．2

  C． 3 2

  D． 3
  组卷：302引用：14难度：0.9

  解析

• 6．设角θ的终边经过点P（-3，4），那么sinθ+2cosθ=（　　）

  A． 1 5

  B． - 1 5

  C． - 2 5

  D． 2 5
  组卷：698引用：19难度：0.9

  解析

• 7．设a=3^0.5，b=log_0.30.5，c=cos3，则a,b,c的大小关系是（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．b＞c＞a

  D．c＞a＞b
  组卷：201引用：4难度：0.7

  解析

四、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

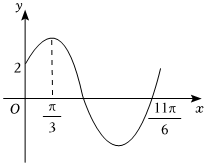• 21．已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜

  π

  2

  ）的部分图象如图所示．
  （1）求f（x）的解析式；
  （2）将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的

  1

  2

  倍，再将所得函数图象向右平移

  π

  6

  个单位，得到函数y=g（x）的图象，求g（x）的单调递增区间；
  （3）当x∈[-

  π

  2

  ，

  5

  π

  12

  ]时，求函数y=f（x+

  π

  12

  ）-

  2

  f（x+

  π

  3

  ）的最值．
  组卷：677引用：9难度：0.3

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  lo

  g

  1

  2

  x

  +

  1

  x

  -

  1

  ．
  （1）判断并证明f（x）的奇偶性；
  （2）若关于x的方程f（x）=log₂（k+x）在（-3，-1）内有实根，求实数k的取值范围；
  （3）已知函数

  g

  （

  x

  ）

  =

  （

  1

  4

  ）

  x

  +

  （

  1

  2

  ）

  x

  -m,若对∀x₁∈[0，1]，∃x₂∈[2，3]，使得g（x₁）≤f（x₂）成立，求实数m的最小值．
  组卷：81引用：4难度：0.3

  解析