2022-2023学年广东省惠州市惠阳区良井中学七年级（上）月考数学试卷（10月份）

一、选择题（共10题，共30分）

• 1．已知a＞b,a＞c,若M=a²-ac,N=ab-bc,则M与N的大小关系是（　　）

  A．M＜N

  B．M=N

  C．M＞N

  D．不能确定
  组卷：1056引用：6难度：0.8

  解析

• 2．下列判断正确的是（　　）

  A．3a2b与ba2不是同类项

  B．单项式-x3y2的系数是-1

  C． m 2 n 5 不是整式

  D．3x2-y+5xy2是二次三项式
  组卷：247引用：9难度：0.9

  解析

• 3．如图是一组有规律的图案，第1个图案由5个基础图形组成，第2个图案由8个基础图形组成，……，如果按照以下规律继续下去，那么通过观察，可以发现：第20个图案需要（　　）个基本图形．
  

  A．402

  B．404

  C．406

  D．408
  组卷：468引用：9难度：0.8

  解析

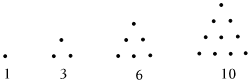• 4．古希腊的毕达哥拉斯学派认为：1，3，6，10，15，21，⋯这些数量的（石子），都可以排成三角形，像这样的数称为三角形，其中，1称为第一个三角形数，3称为第二个三角形数，以此类推，那么，第23个三角形数与第21个三角形数的差为（　　）

  A．23

  B．24

  C．45

  D．47
  组卷：10引用：2难度：0.5

  解析

• 5．按一定规律排列的单项式：a,-a²，a³，-a⁴，a⁵，-a⁶，…，第n个单项式是（　　）

  A．an

  B．-an

  C．（-1）n+1an

  D．（-1）nan
  组卷：2109引用：25难度：0.9

  解析

• 6．如图，下面是按照一定规律画出的“数形图”，经观察可以发现：图A₂比图A₁多出2个“树枝”，图A₃比图A₂多出4个“树枝”，图A₄比图A₃多出8个“树枝”，……，照此规律，图A₆比图A₂多出的“树枝”的个数是（　　）
  

  A．28个

  B．56个

  C．60个

  D．124个
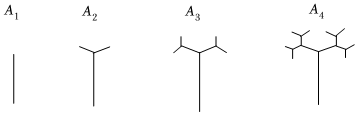  组卷：41引用：4难度：0.7

  解析

• 7．为了求1+2+2²+2³+…+2²⁰¹¹+2²⁰¹²的值，可令S=1+2+2²+2³+…+2²⁰¹¹+2²⁰¹²，则2S=2+2²+2³+2⁴+…+2²⁰¹²+2²⁰¹³，因此2S-S=2²⁰¹³-1，所以1+2²+2³+…+2²⁰¹²=2²⁰¹³-1．仿照以上方法计算1+5+5²+5³+…+5²⁰¹²的值是（　　）

  A．52013-1

  B．52013+1

  C． 5 2013 - 4 4

  D． 5 2013 - 1 4
  组卷：14565引用：19难度：0.1

  解析

• 8．当x=1时，多项式ax⁵+bx³+cx-1的值是5，则当x=-1时，它的值是（　　）

  A．-7

  B．-3

  C．-5

  D．7
  组卷：506引用：6难度：0.6

  解析

三、解答题（共8题，共62分）

• 24．阅读下列材料并解决问题：
  若一个正整数满足：个位数字不为0，将原数各个数位上的数字从个位到高位依序重排得到一个新数，将新数与原数相加，所得的和能被15整除，则称这个数为“优数”．
  例如：327是“优数”，因为327+723=1050，且1050÷15=70；35不是“优数”，因为35+53=88，而88不能被15整除．
  （1）判断87、139是否为“优数”，并说明理由；
  （2）若一个三位正整数M是“优数”，且满足个位数字大于百位数字，则称M为“最优数”．请求出“最优数”的个数．
  组卷：1037引用：3难度：0.3

  解析

• 25．已知：△ABC中，BC=a,AC=b,AB=c,a是最小的合数，b、c满足等式：|b-5|+（c-6）²=0，点P是△ABC的边上一动点，点P从点B开始沿着△ABC的边按BA→AC→CB顺序顺时针移动一周，回到点B后停止，移动的路径为S，移动的速度为每秒3个单位．如图1所示．
  （1）试求出△ABC的周长；
  （2）当点P移动到AC边上时，化简：|S-4|+|3S-6|+|4S-45|；
  （3）如图2所示，若点Q是△ABC的边上一动点，P、Q两点分别从B、C同时出发，即当点P开始移动的时候，点Q从点C开始沿着△ABC的边顺时针移动，移动的速度为每秒5个单位，试问：当t为何值时，P、Q两点的路径（在三角形的边上的距离）相差为3？此时点P在△ABC的哪条边上？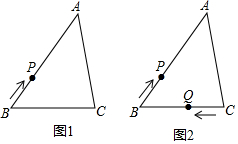
  
  组卷：274引用：3难度：0.5

  解析