阅读下列材料并解决问题:
若一个正整数满足:个位数字不为0,将原数各个数位上的数字从个位到高位依序重排得到一个新数,将新数与原数相加,所得的和能被15整除,则称这个数为“优数”.
例如:327是“优数”,因为327+723=1050,且1050÷15=70;35不是“优数”,因为35+53=88,而88不能被15整除.
(1)判断87、139是否为“优数”,并说明理由;
(2)若一个三位正整数M是“优数”,且满足个位数字大于百位数字,则称M为“最优数”.请求出“最优数”的个数.
【考点】因式分解的应用.
【答案】见试题解答内容
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/8 11:0:12组卷:1037引用:3难度:0.3
相似题
-
1.已知x-y=2,
=1,求x2y-xy2的值.1x-1y发布:2025/5/25 14:0:1组卷:1946引用:12难度:0.6 -
2.一个四位正整数P满足千位上的数字比百位上的数字大2,十位上的数字比个位上的数字大2,千位上的数字与十位上的数字不相等且各个数位上的数字均不为零,则称P为“双减数”,将“双减数”P的千位和十位数字组成的两位数与百位和个位数字组成的两位数的和记为M(P),将“双减数”P的千位和百位数字组成的两位数与十位和个位数字组成的两位数的差记为N(P),并规定F(P)=
.M(P)N(P)
例如:四位正整数7564,∵7-5=6-4=2,且7≠6,∴7564是“双减数”,此M(7564)=76+54=130,N(7564)=75-64=11,∴F(7564)=.13011
(1)填空:F(3186)=,并证明对于任意“双减数”A,N(A)都能被11整除;
(2)若“双减数”P为偶数,且M(P)-N(P)能被6整除,求满足条件的所有“双减数”P,并求F(P)的值.发布:2025/5/25 17:0:1组卷:383引用:2难度:0.5 -
3.【实践操作】
小明在学习了八下数学课本中“因式分解”章节,用各若立体方块进行实践操作探究,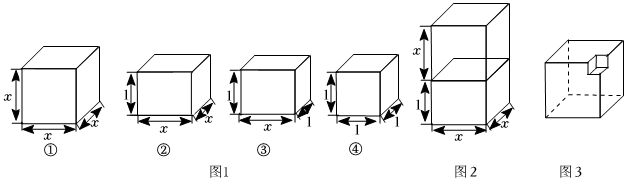
【温故知新】
如图,现有编号为①②③④的四种长方体各若干块,现取其中两块拼成一个大长方体如图2,据此写出一个多项式的因式分解:.
【问题解决】
如图,若要用这四种长方体拼成一个棱长为(x+1)的正方体,需要②号长方体 个,③号长方体 个,据此写出一个多项式的因式分解:.
【拓展与延伸】
如图3,在一个棱长为a的正方体中挖出一个棱长为b的正方体,据此写出a3-b3=.发布:2025/5/25 16:0:2组卷:217引用:2难度:0.4


