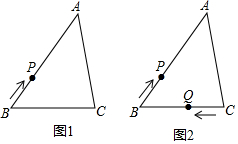
已知：△ABC中，BC=a,AC=b,AB=c,a是最小的合数，b、c满足等式：|b-5|+（c-6）2=0，点P是△ABC的边上一动点，点P从点B开始沿着△ABC的边按BA→AC→CB顺序顺时针移动一周，回到点B后停止，移动的路径为S，移动的速度为每秒3个单位．如图1所示．
（1）试求出△ABC的周长；
（2）当点P移动到AC边上时，化简：|S-4|+|3S-6|+|4S-45|；
（3）如图2所示，若点Q是△ABC的边上一动点，P、Q两点分别从B、C同时出发，即当点P开始移动的时候，点Q从点C开始沿着△ABC的边顺时针移动，移动的速度为每秒5个单位，试问：当t为何值时，P、Q两点的路径（在三角形的边上的距离）相差为3？此时点P在△ABC的哪条边上？
【考点】三角形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/8 11:0:12组卷：274引用：3难度：0.5
相似题
-
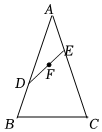1．如图，△ABC是等腰三角形，AB=AC=5，∠BAC是锐角．点D从点A向点B运动，点E是AC上一动点，在运动过程中保持AD=CE，连接DE，若，则在点D运动的过程中，线段DE的中点F的运动路径长是 ．S△ABC=152发布：2025/5/25 17:0:1组卷：127引用：1难度：0.4 -
2．如图，在△ABC中，∠BAC=90°，AB=AC，点D在边AC上，点E在线段BD上，连接AE，且AE=BE，延长AE交BC于点F，过点A作AG⊥AE交BD的延长线于点G．
（1）①若∠GBC=30°，则∠AEG=°；②如图1，求证：∠AGB=2∠GBC；
（2）如图2，连接CG，若∠BGC=90°，求证：BG平分∠ABC；
（3）如图3，若AF=AG，求证：D是AC的中点．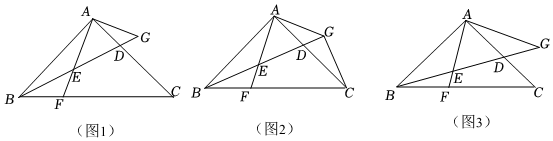
发布：2025/5/25 17:0:1组卷：201引用：1难度：0.3 -
3．已知：在△ABC中，AB=AC，∠BAC=120°，点F是线段BC上一点，D、E是射线AF上两点，且∠ADB=∠BAC，∠AEC=60°．
（1）如图1，
①填空：∠BAE ∠ACE；（填“＞”或“=”或“＜”）
②判定三条线段AD，BD，CE的数量关系，并说明理由；
（2）若∠DBC=15°，则直接写出的值．FCBF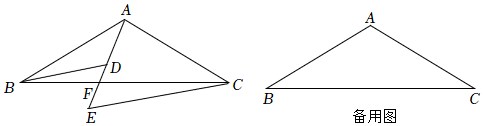
发布：2025/5/25 17:30:1组卷：278引用：3难度：0.1
