当前位置：试卷中心 > 试卷详情

2022-2023学年安徽省亳州市第二完全中学高一（下）期末数学试卷（A卷）

发布：2024/6/18 8:0:10

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1．复数z满足i²⁰²³（2+z）=2-i,则
z
=（　　）
A．-1+2i B．1+2i C．-1-2i D．1-2i
组卷：282引用：10难度：0.7
解析
2．两个粒子A，B从同一发射源发射出来，在某一时刻，它们的位移分别为
s
A
=
（
4
，
3
）
，
s
B
=
（
-
2
，
6
）
，则
s
B
在
s
A
上的投影向量的长度为（　　）
A．10 B．
10
2
C．
10
10
D．2
组卷：201引用：4难度：0.7
解析
3．已知向量
a
=
（
sinθ
，
1
）
，
b
=
（
cosθ
，
2
）
，若
a
∥
b
，则tan2θ=（　　）
A．
4
3
B．
-
4
3
C．
1
2
D．
-
1
2
组卷：59引用：2难度：0.8
解析
4．已知l,m,n是三条不同的直线，α，β，γ是三个不同的平面，则下列结论正确的是（　　）
A．若α∥β，l∥α，则l∥β
B．若m⊂α，n⊂α，l⊥m,l⊥n,则l⊥α
C．若β⊥α，γ⊥α，则β∥γ
D．若m⊥α，n⊥α，l∥m,则l∥n
组卷：44引用：3难度：0.5
解析
5．已知角α为第一象限角，且
sin
α
2
＞
cos
α
2
，则
sin
α
2
的取值范围是（　　）
A．
（
-
2
2
，
0
）
B．
（
-
1
，-
2
2
）
C．
（
0
，
2
2
）
D．
（
2
2
，
1
）
组卷：466引用：4难度：0.8
解析
6．在△ABC，其内角A，B，C的对边分别为a,b,c,若acosAcosB+bcos²A=acosA，则△ABC的形状是（　　）
A．直角三角形 B．等腰三角形
C．.等腰直角三角形 D．等腰或直角三角形
组卷：715引用：12难度：0.7
解析
7．若sin2α=
5
5
，sin（β-α）=
10
10
，且α∈[
π
4
，π]，β∈[π，
3
π
2
]，则α+β的值是（　　）
A．
7
π
4
B．
9
π
4
C．
5
π
4
或
7
π
4
D．
5
π
4
或
9
π
4
组卷：6534引用：41难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

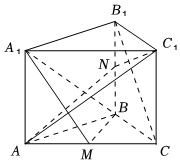21．如图，在直三棱柱ABC-A₁B₁C₁中，M为棱AC的中点，AB=BC，AC=2，AA₁=
2
．
（1）求证：B₁C∥平面A₁BM；
（2）求证：AC₁⊥平面A₁BM；
（3）在棱BB₁上是否存在点N，使得平面AC₁N⊥平面AA₁C₁C？如果存在，求此时
BN
B
B
1
的值；如果不存在，请说明理由．
组卷：381引用：7难度：0.6
解析
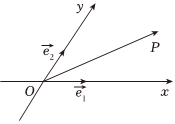22．我们把由平面内夹角成60°的两条数轴Ox,Oy构成的坐标系，称为“@未来坐标系”．如图所示，
e
1
，
e
2
两分别为Ox,Oy正方向上的单位向量．若向量
OP
=
x
e
1
+
y
e
2
，则把实数对（x,y）叫做向量
OP
的“@未来坐标”，记
OP
=
{
x
,
y
}
．已知{x₁，y₁}，{x₂，y₂}分别为向量
a
，
b
的@未来坐标．
（1）证明：{x₁，y₁}•{x₂，y₂}=x₁x₂+y₁y₂+
1
2
（x₁y₂+x₂y₁）；
（2）若向量
a
，
b
的“@未来坐标”分别为{sinx,1}，{cosx,1}，已知
f
（
x
）
=
a
•
b
，x∈R，求函数f（x）的最值．
组卷：11引用：2难度：0.6
解析