2022-2023学年江西省赣州市龙南中学高一（下）期末数学试卷

一、单选题（每题5分，共40分）

• 1．sin210°cos120°的值为（　　）

  A． 1 4

  B．- 3 4

  C．- 3 2

  D． 3 4
  组卷：253引用：11难度：0.9

  解析

• 2．若

  sin

  （

  π

  -

  α

  ）

  =

  6

  3

  ，则

  cos

  （

  3

  π

  2

  -

  α

  ）

  =（　　）

  A． - 6 3

  B． - 3 3

  C． 6 3

  D． ± 6 3
  组卷：409引用：3难度：0.8

  解析

• 3．已知向量

  a

  =

  （

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  3

  ，

  1

  ）

  ，则向量

  a

  在向量

  b

  方向上的投影向量是（　　）

  A． - b 10

  B． b 10

  C． - 10 10 b

  D． 10 10 b
  组卷：127引用：4难度：0.8

  解析

• 4．在△ABC中，D点为边BC中点，记

  AB

  =

  a

  ，

  AC

  =

  b

  ，则

  AD

  =（　　）

  A．2（ a + b ）

  B．2（ a - b ）

  C． 1 2 （ a - b ）

  D． 1 2 （ a + b ）
  组卷：134引用：8难度：0.7

  解析

• 5．已知m,n是两条不同的直线，α是一个平面，则下列命题是真命题的为（　　）

  A．若m∥n,n⊂α，则m∥α

  B．若m⊥α，m∥n,则n⊥α

  C．若m∥α，n∥α，则m∥n

  D．若α⊥β，α∩β=m,n⊥m,则n⊥α
  组卷：39引用：3难度：0.7

  解析

• 6．函数f（x）=cosx-cos2x,试判断函数的奇偶性及最大值（　　）

  A．奇函数，最大值为2	B．偶函数，最大值为2
  C．奇函数，最大值为 9 8	D．偶函数，最大值为 9 8
  组卷：746引用：8难度：0.7

  解析

• 7．在正四棱台ABCD-A₁B₁C₁D₁中，AB=2A₁B₁=4，侧棱

  A

  A

  1

  =

  6

  ，若P为B₁C₁的中点，则过B，D，P三点截面的面积为（　　）

  A． 15 2

  B． 4 6

  C． 5 3

  D． 6 2
  组卷：210引用：5难度：0.6

  解析

四、解答题（共70分）

• 21．已知复数

  z

  1

  =

  2

  sinθ

  -

  3

  i

  ,

  z

  2

  =

  1

  +

  （

  2

  cosθ

  ）

  i

  ,

  i

  为虚数单位．
  （1）若

  θ

  ∈

  [

  0

  ，

  π

  2

  ]

  ，且z₁•z₂为实数，求θ的值；
  （2）若

  θ

  ∈

  [

  π

  2

  ，

  5

  π

  6

  ]

  ，复数z₁z₂对应的向量分别是

  a

  、

  b

  ，存在θ使等式

  （

  λ

  a

  -

  b

  ）

  •

  （

  a

  -

  λ

  b

  ）

  =

  0

  成立，求实数λ的取值范围．
  组卷：128引用：3难度：0.6

  解析

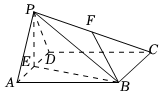• 22．如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°，△PAD是正三角形，E为线段AD的中点，点F为棱PC上的动点．
  （1）求证：平面PBC⊥平面PBE；
  （2）若平面PAD⊥平面ABCD．
  ①当点F恰为PC中点时，求异面直线PD与BF所成角的余弦值；
  ②在平面PBE内确定一点H，使CH+FH的值最小，并求此时

  BH

  BP

  的值．
  组卷：203引用：5难度：0.5

  解析